用TwoSampleMR包做孟德尔随机化分析

发表于 更新于 分类于

如题。

一、为什么要做孟德尔随机化

一言以蔽之：相关性 ≠ 因果性。

在研究中我们常常观察到一些相关性，例如人群中某个基因与某种疾病的发病率正相关。然而这种相关性并不能解释基因和疾病的关联，有可能是基因产物造成了这种疾病（真因果），有可能是这个基因的连锁基因的产物造成了疾病，甚至有可能是疾病的病因（例如逆转录病毒的感染）造成了这个基因的异常……

相关性说明不了因果性，因为存在第三种或更多因素，而造成相关性的情况也有很多种。简单概括一下，下面这些情况都会造成相关性：

  • 因果相关：A导致B，B导致C  (A→B→C)
  • 混杂相关：A导致B跟C，造成B和C相关  (A→B,A→C)
  • 对撞相关：A跟B共同导致C，控制C后A跟B相关  (A→C,B→C,(C):A→B)
  • 随机相关：高维度数据中碰巧两个变量表现出了相关性

孟德尔随机化方法是一种因果分析方法，灵感来源于经济学研究中的工具变量分析。它可以区分上述这些情况，并正确估计或探索变量间的关系。

二、孟德尔随机化的原理

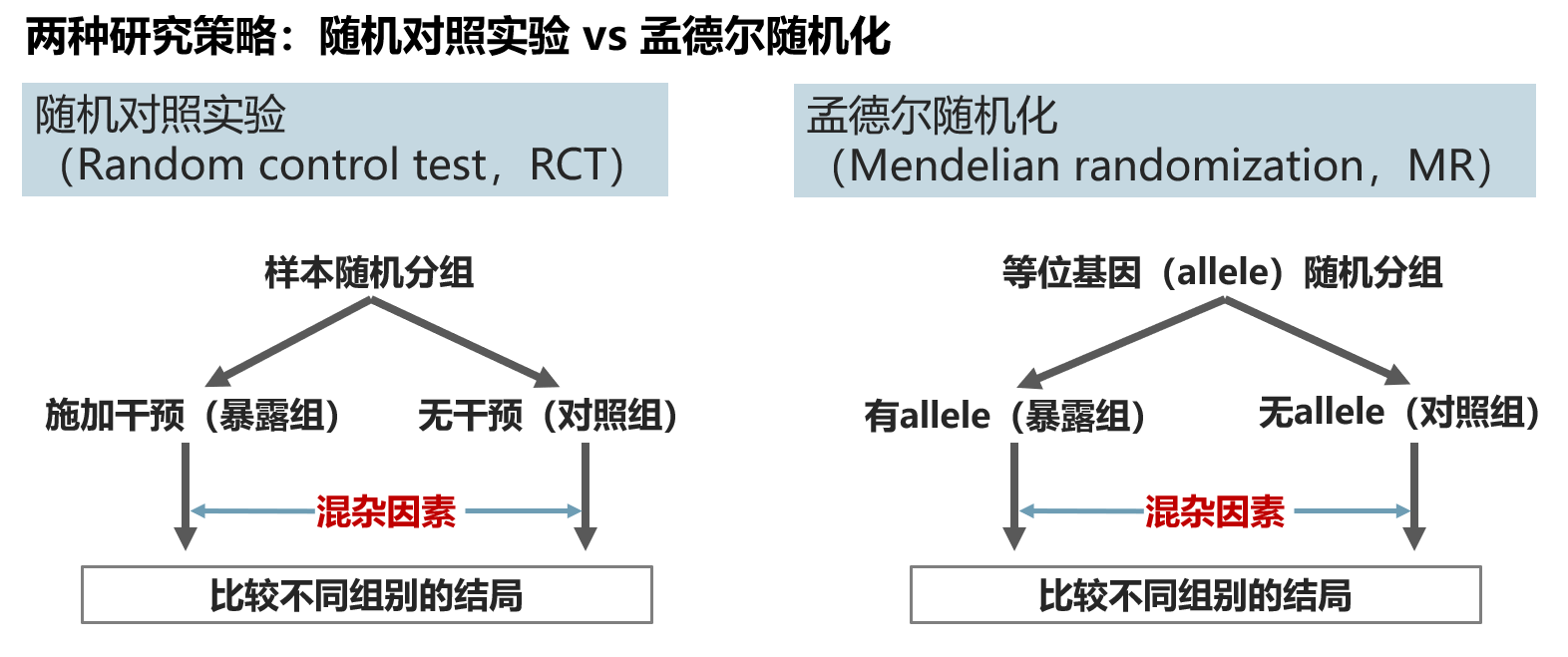
image.png

如上图。

某种意义上说，随机对照实验（RCT）更能揭示因果关系。然而RCT需要实验，成本很高。
孟德尔随机化（MR）的思路与CRT一致，但“随机分组”的过程由孟德尔分离定律所代替，因此无需实验，可以仅凭观察数据得出结论，实验成本更低，并且保证了最终结论的准确性。

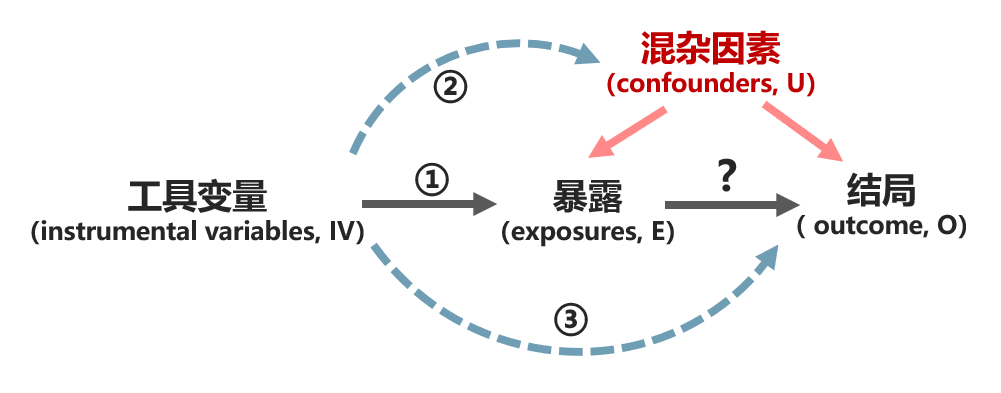
image.png

孟德尔随机化主要用于确定暴露因素（E）和结局（O）之间的因果关系。为了排除混杂因素的干扰，需要引入工具变量（IV），在此次是与且仅与暴露相关的一组遗传变异。作为工具变量的遗传变异满足下面三个核心假设：

  • 1、关联性假设：工具变量（IV）与暴露（E）存在关联（图中①）
  • 2、独立性假设：工具变量（IV）与混杂因素（U）不存在关联（图中②）
  • 3、排他性假设：工具变量（IV）与结局（O）没有任何关联（图中③），除非通过暴露（E）（图中IV→E→O）

例如，我们想要研究咖啡因摄入如何影响肾结石发病率，可以这样选择：

  • 工具变量（IV）：通过GWAS找到的一组与咖啡因摄入有关的SNP
  • 暴露（exposure）：咖啡因摄入水平
  • 结局（outcome）：肾结石发病率

有多种方法可以用于计算MR，这些方法包括Wald ratio方法、逆方差加权法（IVW）、MR-Egger法等。不同方法有不同的适用情景，如果工具变量数量太少（只有一两个），那么Wald ratio方法会很合适。当有多个工具变量时，我们可以对每个工具变量各自计算Wald ratio，最后进行加权求和，这就是逆方差加权法（IVW）和MR-Egger法的原理。

有多种工具可以方便我们计算MR，下面我们只介绍一种：TwoSampleMR

三、TwoSampleMR包的安装与使用

TwoSampleMR包是一个用R语言编写的MR计算工具，其连接到了IEU GWAS database的后端，因此可以很方便的进行工具变量选取。

TwoSampleMR包暂时没有被CRAN收录，但作者提供了GitHub安装方法。在R语言的交互环境中输入下面的指令即可进行安装：

1
2
install.packages("remotes")
remotes::install_github("MRCIEU/TwoSampleMR")

如果网络不太好，也可也从上述GitHub存储库中的release页面上直接下载.tar.gz格式的源码包，然后在R语言交互式环境中使用下面的指令进行源码包安装：

1
install.packages("TwoSampleMR-0.5.10.tar.gz",repo=NULL,type="source")

此外，TwoSampleMR 包依赖于 RadialMR 包（ https://github.com/WSpiller/RadialMR ），因此如果上述安装方法出现问题，可以尝试先安装RadialMR包：

1
remotes::install_github("WSpiller/RadialMR")

然后再安装TwoSampleMR。

使用方法也很简单。下面这个例子来自TwoSampleMR的官方文档，研究的是身体质量指数（BMI）与冠心病（CDH）风险的因果关系。其中，BMI是暴露，而CDH是结局，我们要寻找一系列与BMI有关的工具变量SNP对这种因果关系进行检验。示例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
library(TwoSampleMR)
# 我们想看一下BMI对冠心病（CDH）风险的因果效应
# 首先选取工具变量
bmi_exp_dat <- extract_instruments(outcomes = 'ieu-a-2', # 选择数据库ID为ieu-a-2研究的SNP，这些是与BMI性状有关的工具变量
                 access_token=NULL) # 如果网络不稳定，可用加上这句话

# 接下来根据工具变量选择结局								   
chd_out_dat <- extract_outcome_data(snps = bmi_exp_dat$SNP, # 筛选含前述工具变量的记录
                 outcomes = 'ieu-a-7', # 选择数据库ID为ieu-a-7的研究，这个研究与CDH相关
                 access_token=NULL) # 同样的，如果网络不稳定，可用加上这句话

# 我们已经获得了一系列的工具变量和与之对应的结局
# 但是，还需要协调一下，以保证SNP对暴露的影响和该SNP对结果的影响对应于同一等位基因。
dat <- harmonise_data(bmi_exp_dat, chd_out_dat)

# 调用MR-Egger方法和IVW方法做MR：
res <- mr(dat,
          method_list = c("mr_egger_regression", "mr_ivw"))
# 展示结果
res

输出：

1
2
3
4
5
6
7
8
9
  id.exposure id.outcome                              outcome
1     ieu-a-2    ieu-a-7 Coronary heart disease || id:ieu-a-7
2     ieu-a-2    ieu-a-7 Coronary heart disease || id:ieu-a-7
                       exposure                    method nsnp         b
1 Body mass index || id:ieu-a-2                  MR Egger   79 0.5024935
2 Body mass index || id:ieu-a-2 Inverse variance weighted   79 0.4459091
          se        pval
1 0.14396056 8.01259e-04
2 0.05898302 4.03202e-14

从输出可以看出，对于BMI这一暴露因素和冠心病（CHD）这一结局，使用MR-Egger方法给出的β值为0.5024935，显著大于0（$p=8.01259^{-4}<0.05$ ），使用IVW方法给出的β值 0.4459091，同样显著大于0（$p=4.03202^{-14}<0.05$ ），这说明BMI对CHD有比较强的正向因果效应。

最后，我们也可也画一个图，展示一下上面的结果：

1
2
res <- mr(dat)
p1 <- mr_scatter_plot(res, dat)

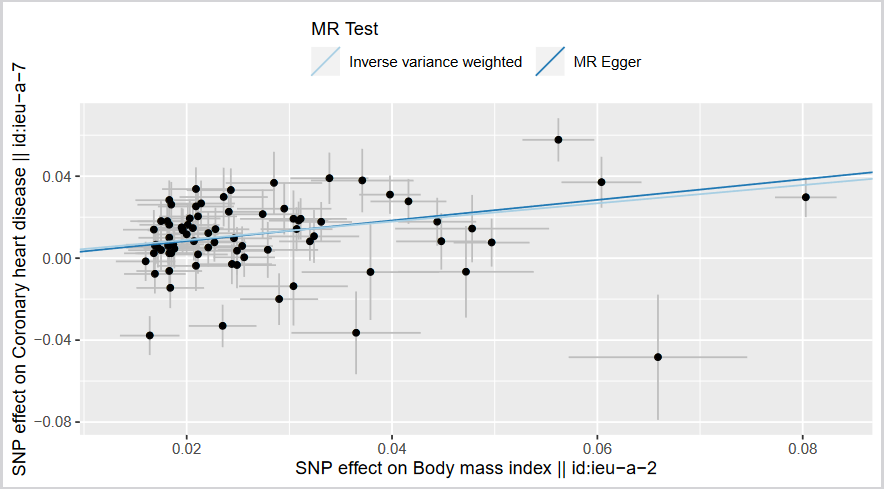
image.png

图中每个点代表一个工具变量对暴露的效应和对结局的效应。加权线性回归拟合出的直线斜率大于1，这说明BMI对CHD有正向因果效应。

参考文献