数学插值与三次样条曲线

发表于 更新于 分类于

本文介绍了样条曲线的原理，以及如何计算三次样条曲线。

一、从插值问题说起

样条函数是一种用于多项式插值的分段函数。

先来解释一下什么是多项式插值。在科学实践中，我们经常会遇到这种情况：采集到了多个样本点，然后对这些样本点进行处理，用一个函数代表这些样本点的特征。一般我们有两种策略去提取这些样本点的特征：（1）拟合（2）插值。拟合不要求方程通过所有的已知点，讲究神似，就是整体趋势一致。插值则是形似，每个已知点都必会穿过，但是高阶会出现龙格现象(Runge Phenomenon) ，所以一般采用分段插值。而样条曲线，特别是分段三次样条曲线，就是一种很常用的插值方法。

龙格现象(Runge Phenomenon) ：对于某些函数，使用均匀节点构造高次多项式差值时，在插值区间的边缘的误差可能很大的现象。如下图所示，蓝线为样本点的真实方程（ $y=1/(1-25\times x^2)$ ，红线为高阶函数插值结果，可以看出其与实际方程差别很大 ）

龙格现象

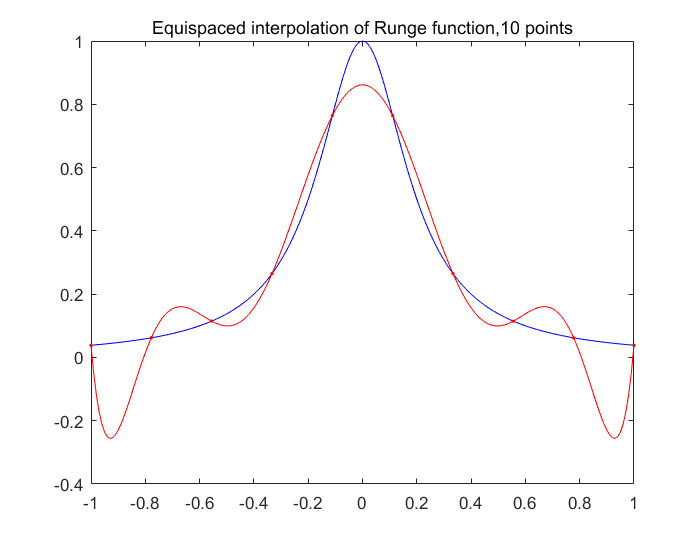
高阶函数插值会出现上述问题，那么另一种方法就是分段函数插值了。最简单的分段函数就是直接用线段连接各个点，但那样得到的曲线并不平滑，各段函数之间有很大的转折。另一种策略就是用曲线进行插值，这就是所谓的样条曲线。

样条曲线（spline）这个词来源于一种在工程制图时用来画出光滑形状的工具，这种工具一般为富有弹性的细木条或薄钢条。由这样的样条形成的曲线在连接点处具有连续的坡度与曲率。

二、三次样条（cubic spline）曲线

如前文所述，要想平滑插值，我们可以在每一段区间使用曲线。例如，我们可以在各段曲线的交界处令插值方程 $S(x)$ 连续，插值方程的一次导函数 $S’(x)$ 连续，二次导 $S’’(x)$ 也连续，从而获得平滑的插值曲线。由此，在每个小区间上，插值函数都是一个三次方程，这就是三次样条曲线函数的由来。

三次样条函数的计算方法如下：

给定区间 $[x_0,x_n]$ 以及属于这一区间的 $n-1$ 个样本点 $x_1,x_2,…,x_{n-1}$ ，我们可以以这些样本点为界将整个区间分为 $n$ 个小段 $[(x_0,x_1),(x_1,x_2),…,(x_{n-1},x_n)]$ 。在这些小段上，三次样条函数满足以下条件：

  • 对于 $\forall i \in [0,n)$ ，在区间 $[x_i,x_{i+1}]$ 上， $S(x)=S_i(x)$ 都是一个三次方程
  • 满足插值条件 $S(x_i)=y_i\ (i=0,1,…,n)$
  • 曲线光滑，即 $S(x),S’(x),S’’(x)$ 连续

则这个三次方程 $S_i(x)$ 可以构造为以下形式：

$$
y=a_i+b_ix+c_ix^2+d_ix^3
$$

在每个小区间 $[x_i,x_{i+1}]$ 上，要求的未知数个数有四个（ $a_i,b_i,c_i,d_i$ ）。有 $n$ 个小区间，因此未知数总数为 $4n$ 。我们需要 $4n$ 个方程求解这些未知数。

幸运的是，根据三次样条函数需要满足的条件，我们可以得到 $4n-2$个方程，其中插值方程 $S(x)$ 连续这一条件可以构造出 $2n$ 个方程，插值方程的一次导函数 $S’(x)$ 连续和二次导函数 $S’’(x)$ 连续各可以构造出 $n-1$ 个方程。还缺少两个方程就可以解出所有未知数，这两个方程由边界条件获得。

对于三次样条函数来说，边界条件有三种：

  • 自然边界 ( Natural Spline )：指定端点二阶导数为0， $S’’(x_0)=S’’(x_n)=0$

  • 固定边界 ( Clamped Spline ): 指定端点一阶导数的值为固定值。

  • 非扭结边界( Not-A-Knot Spline ): 强制第一个插值点的三阶导数值等于第二个点的三阶导数值，最后第一个点的三阶导数值等于倒数第二个点的三阶导数值。

三种边界条件的区别如下图所示。可以看出，自然边界和非扭结边界看起来更自然一点。

边界条件

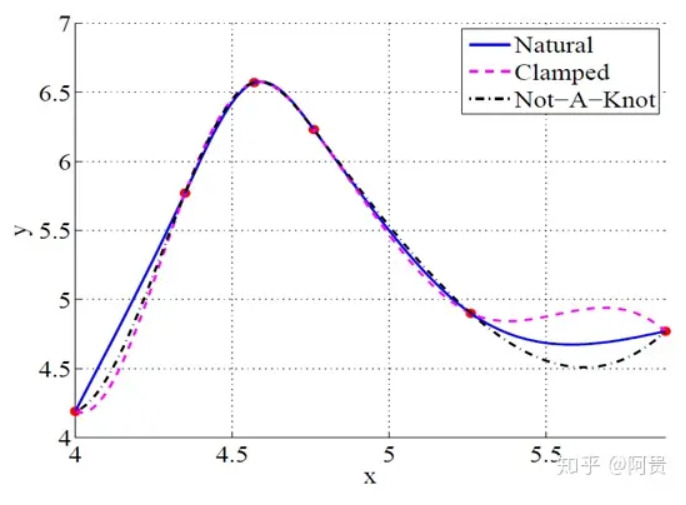
如此，我们得到了 $4n$ 个方程组，可以解对应的 $4n$ 个方程系数。具体推导略，主要涉及多元一次函数的解法，或者参考文章：《三次样条（cubic spline）插值》。总之在确定方程以后，主要工作就是解方程组。

三、代码方法求解三次样条曲线

scipy库是一个强大的科学计算函数库，其中提供了interpolate模块，实现了多种插值方法。其中，scipy.interpolate.CubicSpline是三次样条插值的官方实现。我们可以使用这一模块来实现插值程序。

下面的程序将接收两个数组作为输入，一个代表样本点的x坐标，另一个代表y坐标，返回一个代表样条曲线系数的矩阵。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import numpy as np
from scipy.interpolate import CubicSpline
import matplotlib.pyplot as plt
# 测试数据
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([0, 1, 0, -1, 0, 1])
# 三次样条函数插值
cs = CubicSpline(x, y)
xs = np.arange(0,5,0.001)
# 绘制图形
plt.plot(xs, cs(xs))
plt.scatter(x,y)
# 获取样条函数的系数
print(cs.c)

插值结果

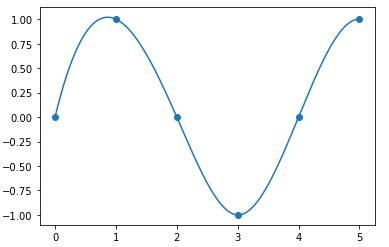
样条函数的系数矩阵：

1
2
3
4
[[ 0.28888889  0.28888889  0.55555556 -0.51111111 -0.51111111]
 [-1.86666667 -1.         -0.13333333  1.53333333  0.        ]
 [ 2.57777778 -0.28888889 -1.42222222 -0.02222222  1.51111111]
 [ 0.          1.          0.         -1.          0.        ]]

四、其他样条曲线

上述方法为三次样条曲线的原理和计算方法。但样条曲线的家族成员还有很多，例如smooth P-spline、bivariate P-spline等。这些样条曲线的计算原理大同小异，并且在不同的领域有重要作用，例如三次样条插值主要用于生成平滑曲线，而平滑P样条和二元P样条更多用于统计建模和分析。

  1. B-spline（基础样条函数）：B-spline是样条函数中最基础且最常用的一种，它是通过一组控制点来定义的，并且具有局部支撑性，即改变一个控制点只会影响到该点附近的曲线形状。B-spline曲线在每个区间内部是多项式函数，通常是三次多项式。本文前述的三次样条曲线即属于这一类函数。
  2. P-spline（惩罚样条函数）：P-spline是”Penalized Spline”的简称，它是一种通过添加惩罚项来增强样条函数光滑性的方法。在P-spline中，我们不仅要求样条函数通过所有的数据点，而且要求样条函数的曲率（二阶导数）尽可能小，以此来增加曲线的光滑性。这个要求是通过在目标函数中添加一个惩罚项来实现的。它的优点是可以自动选择平滑参数，而且计算速度较快。它的缺点是可能对数据的噪声敏感，而且不能很好地处理不规则的网格数据
  3. S-spline（光滑样条函数）：S-spline是”Smoothing Spline”的简称。与P-spline类似，S-spline也是通过最小化一个包含惩罚项的目标函数来求解样条函数的。不过，S-spline通常用于非参数回归中，它的目标是找到一个函数，该函数在拟合数据的同时，也使得函数本身的粗糙度（即曲线的弯曲程度）最小。

总的来说，这三种样条函数的主要区别在于如何权衡拟合精度和光滑性。B-spline是最基础的样条函数，它不包含任何惩罚项，因此它的形状完全取决于控制点。P-spline和S-spline则通过添加惩罚项来增加 光滑性，但它们的目标函数和求解方法略有不同。

参考：