信息论学习笔记(八)
前段时间查文献的时候,偶然看到了一些算法里涉及到了信息论的相关知识。信息论我在几年前通过看书自学过,时间太久有些忘了,正好趁此机会重新复习一下。
参考书籍:机械工业《信息论基础(原书第二版)》(ELEMENTS OF INFORMATION THEORY SECOND EDITION),作者Thomas M. Cover, Joy A. Thomas
微分熵
微分熵定义
微分熵是一个连续随机变量的熵。
- 定义:设 $X$ 是一个随机变量,其累积分布函数 $F(x) = P_r(X \leq x)$。若 $F(x)$ 连续,则称该随机变量是连续的。
- 概率密度函数:当 $F(x)$ 导数存在时,记 $f(x) = F’(x)$。若 $\int_{-\infty}^{\infty} f(x) dx = 1$,则称 $f(x)$ 为 $X$ 的 概率密度函数。
- 支持集:使 $f(x) > 0$ 的所有 $x$ 构成的集合称为 $X$ 的 支持集。
连续随机变量的微分熵
一个以 $f(x)$ 为概率密度函数的连续型随机变量 $X$ 的微分熵 $h(X)$ 定义为:
$$h(X) = -\int_S f(x) \log f(x) dx$$
其中, $S$ 是 $X$ 的支持集。
考虑一个区间 $[0, a]$ 上的均匀分布:$h(X) = -\int_0^a \frac{1}{a} \log \frac{1}{a} dx = \log (a)$
- 非负性:当 $a < 1$ 时,$h(X) < 0$,即微分熵可以是负的。
- 非负指数性质:但无论如何,$2^{h(X)} = 2^{log(a)} = a$ 总是非负的。
连续随机变量的 AEP(典型序列)
- 定义:集合 $A \subseteq \mathbb{R}^n$ 的体积 $\text{Vol}(A) = \int_A dx_1 dx_2 \cdots dx_n$
- **典型集 $A_\varepsilon^{(n)}$**:具有以下性质:
- 对于充分大的 $n$,$P_r(A_\varepsilon^{(n)}) > 1 - \varepsilon$
- 对于所有的 $n$,$\text{Vol}(A_\varepsilon^{(n)}) \leq 2^{n(h(X) + \varepsilon)}$
- 对于充分大的 $n$,$\text{Vol}(A_\varepsilon^{(n)}) \geq (1 - \varepsilon) 2^{n(h(X) - \varepsilon)}$
在一阶指数意义下,在所有概率 $≥1-ε$ 的集合 $\phi$ 中, $A_\epsilon^{(n)}$ 是体积最小者。
熵的近似:如果随机变量 $X$ 的密度函数 $f(x)$ 是黎曼可积的,那么:
$$H(X^\Delta) + \log \Delta \to h(f) = h(X), \text{ 当 } \Delta \to 0$$
于是,连续随机变量X经过X比特量化处理(此时分割的小区间长度 $\frac{1}{2^n}$ )之后,熵大约是 $h(x)+n$ 。
联合微分熵与条件微分熵
- 联合微分熵:
$$h(X_1, X_2, \ldots, X_n) = -\int f(x^n) \log f(x^n) dx^n$$ - 条件微分熵:
$$h(X|Y) = -\int f(x,y) \log f(x|y) dxdy = h(X,Y) -h(Y)$$
- 多元正态分布 $N(\mu, K)$ 的熵:
$$h(X) = \frac{1}{2} \log ((2\pi e)^n |K|) \text{ bit}$$
相对熵与互信息
- 相对熵:
$$D(f | g) = \int f \log \frac{f}{g}$$
(只有当 $f$ 的支持集包含在 $g$ 的支持集中时,$D(f | g)$ 才是有意义的。) - 互信息:$$I(X; Y) = \int f(x,y) \log \frac{f(x,y)}{f(x)f(y)} dxdy$$
$$I(X; Y) = h(X) - h(X|Y) = h(Y) - h(Y|X) = h(X) + h(Y) - h(X,Y)$$
$$I(X; Y) = D(f_{X,Y} | f_X f_Y)$$
一些性质
- 非负性:$D(f | g) \geq 0$
- 链式法则:$h(X_1, X_2, \ldots, X_n) = \sum_{i=1}^n h(X_i | X_1, X_2, \ldots, X_{i-1})$
- 平移不变性:$h(X + c) = h(X)$(平移不改变微分熵)
- 尺度变换:$h(aX) = h(X) + \log |a|$
- 高斯随机向量的熵:若 $X \in \mathbb{R}^n$ 的均值为 0 ,协方差矩阵 $K = E[XX^T]$,则:
$$h(X) \leq \frac{1}{2} \log ((2\pi e)^n |K|)$$
当且仅当 $X \sim N(0, K)$ 时取等。 - 估计误差:$E(X - \hat{X})^2 \geq \frac{1}{2\pi e} e^{2h(X)}$
当且仅当 $X$ 为高斯分布且 $\hat{X}$ 为其均值时等号成立。
有效字母表大小
- $2^{H(X)}$ 为一个高斯随机变量的有效字母表大小。
- $2^{h(X)}$ 为一个连续随机变量的有效支持集大小。
- $2^C$ 为一个信道容量为 $C$ 的信道的有效字母表大小。
高斯信道
基本模型

高斯信道:输入输出关系为 $Y_i = X_i \oplus Z_i$ ,其中:
- $X_i$ 是时刻 $i$ 的输入信号;
- $Z_i \sim \mathcal{N}(0, N)$ 是加性高斯白噪声(AWGN)。
若噪声方差 $N = 0$ ,则信道容量为无限大。
功率受限的高斯信道容量
问题:在噪声方差为 $N$ 且平均功率约束为 $P$ (我们令 $\frac{1}{n} \sum_{i=1}^n X_i^2 \leq P$ )的条件下,求高斯信道的容量,即最大互信息 $I(X; Y)$ 。
结论:
$$
C = \max_{p(x)} I(X; Y) = \frac{1}{2} \log \left( 1 + \frac{P}{N} \right)
$$
$\Rightarrow$ 高斯信道容量 由信噪比$\frac{P}{N}$决定。

一次发送1bit信息的错误概率: 假设发送二进制消息 $b \in {0, 1}$ ,对应输入 $X = \sqrt{P}$ 或 $-\sqrt{P}$:
$$
P_e = \frac{1}{2} P_r(Y < -\sqrt{P} | X = \sqrt{P}) + \frac{1}{2} P_r(Y > \sqrt{P} | X = -\sqrt{P})
$$
$\Rightarrow$ 错误概率为:
$$
P_e = Q\left( \sqrt{\frac{2P}{N}} \right)
$$
其中$Q(\cdot)$是标准正态分布的尾部概率函数。
高斯信道的码结构与可达性
码的要素
一个功率限制为 $P$ 的高斯信道所对应的 $(M, n)$ 码由以下几个要素构成:
- 下标集:${1, 2, \cdots, M}$
- 编码函数:$x: {1, 2, \cdots, M} \rightarrow x^n$,相应的码字 $x^n(1), x^n(2), \cdots, x^n(M)$ ,且满足功率限制 $P$,即对每个码字,$\frac{1}{n} \sum_{i=1}^n x_i^2(w) \leq P$,$w = 1, 2, \cdots, M$。
- 译码函数:$g: \mathcal{Y}^n \rightarrow {1, 2, \cdots, M}$
- 误差概率的算术平均:$P_e^{(n)} = \frac{1}{2^{nR}} \sum \lambda_i$
码的可达性
对于一个功率限制为 $P$ 的高斯信道,若存在码字功率限制的一个 $(2^{nR}, n)$ 码序列使得最大误差概率 $\lambda^n \rightarrow 0$,则称码率为 $R$ 关于该功率限制为 $P$ 的高斯信道是 可达的。
带宽有限信道
信道表达式:
$Y(t) = (X(t) + Z(t)) * h(t)$
- $X(t)$:信号波形
- $Z(t)$:高斯白噪声
- $h(t)$:理想的低通滤波器(过滤频率大于 $W$ 的所有频率)
采样定理:以采样频率 $\frac{1}{2W}$ 进行采样,足以重构信号。
噪声特性:
- 噪声的功率谱密度为 $\frac{N_0}{2}$ W/Hz
- 带宽 $W$ Hz
- 其功率为 $\frac{N_0}{2} \cdot 2W = N_0 W$
每样本容量:
$C = \frac{1}{2} \log \left( 1 + \frac{P}{N_0} \right)= \frac{1}{2} \log \left( 1 + \frac{P}{\frac{N_0}{2} \cdot 2W} \right) = \frac{1}{2} \log \left( 1 + \frac{P}{N_0 W} \right)$
信道容量:
$C = W \log \left( 1 + \frac{P}{N_0 W} \right)$
- $N_0/2$:噪声谱密度
- $P$:功率
- 每秒有 $2W$ 个样本, 信道容量 = $2W \times$ 每样本容量
- **若 $W \to \infty$**:$C = \frac{P}{N_0} \log_2 e \quad (\text{bit/s})$
- 对于无限带宽信道,信道容量与功率成线性增长关系。
- 以电话线路为例: 带宽 $W = 3300$ Hz ,响度 $33$ dB(即 $\frac{P}{N_0 W} = 2000$),则 $C = W \log \left( 1 + \frac{P}{N_0 W} \right) = 3300 \log \left( 1 + 2000 \right) \approx 36 \text{ kbps}$
并联高斯信道
- 模型:多个独立子信道 $Y_j = X_j + Z_j$ ,$j = 1, 2, \ldots, K$ ,其中 $Z_j \sim \mathcal{N}(0, N_j)$ 。
- 总容量:
$$
C \le \sum_{j=1}^K \frac{1}{2} \log \left( 1 + \frac{P_j}{N_j} \right)
$$
$\Rightarrow$ 总容量等于各子信道容量之和。
- 功率分配策略: 注水法(Water-Filling), 在满足总功率约束$\sum_{j=1}^K P_j \leq P$下,最优功率分配为:
$$
P_j = \left( \nu - {N_j} \right)^+
$$
即对 $P_i$ 取正的部分,而负的部分设为0(公式中的 $\nu$ 由总功率约束确定 )。注水法的直观理解是优先分配功率给噪声小的信道(如下图)。

高斯彩色噪声信道(噪声互相相关)
- $K_z$ 为噪声的协方差阵。
- $K_x$ 为输入信号的协方差阵。
- 功率限制: $\frac{1}{n} \sum_{i=1}^n E[X_i^2] \leq P \Leftrightarrow \frac{1}{n} \text{tr}(K_x) \leq P$
- 互信息表达式 $I(X_1, X_2, \cdots, X_n; Y_1, Y_2, \cdots, Y_n) = h(Y_1, Y_2, \cdots, Y_n) - h(Z_1, Z_2, \cdots, Z_n)$ ,我们的目标是最大化此表达式中的 $h(Y_1, Y_2, \cdots, Y_n)$ 项,因为后一项 $h(Z_1, Z_2, \cdots, Z_n)$ 由噪声分布唯一决定。
- $h(Y_1, Y_2, \cdots, Y_n)= \frac{1}{2} \log((2\pi e)^n |K_x + K_z|)$ ,问题简化为在 $K_x$ 约束下,选择 $K_x$,最大化 $|K_x + K_z|$
- 分解 $K_z$ 为对角型:$K_z = Q \Lambda Q^t$,其中 $QQ^t = I$
- **则 $|K_x + K_z| = |K_x + Q \Lambda Q^t| = |Q^t K_x Q + \Lambda| = |A + \Lambda|$**,其中 $A = Q^t K_x Q$
- 可证明 $\Pi (A_{ii} + \lambda_i)$ 在 $A_{ii} + \lambda_i = v$ 时取最大,且 $A_{ii}$ 可能为负。 $\Rightarrow A_{ii} = (v - \lambda_i)^+$ ,选取 $v$ 使得 $\sum A_{ii} = nP$ ,即下图的频域注水法。
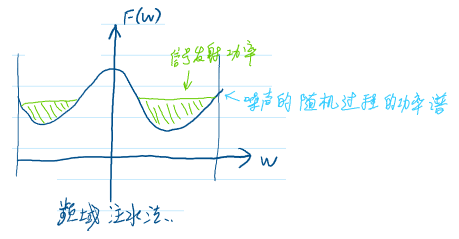
- 一个噪声功率谱为 $N(f)$ 的可加高斯噪声信道的容量: $C = \int_{-\infty}^{\infty} \frac{1}{2} \log \left( 1 + \frac{(\psi - N(f))^+}{N(f)} \right) df$ , 其中 $\psi$ 满足 $\int (\psi - N(f))^+ df = P$
带反馈的高斯信道
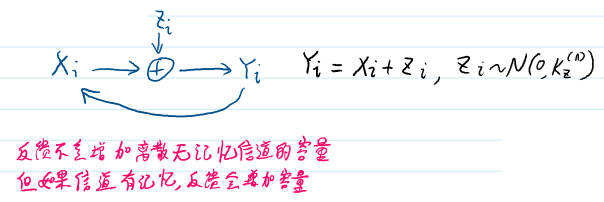
信道表达式: $Y_i = X_i \oplus Z_i, Y_i \xrightarrow{\text{反馈}} X_i, \quad Z_i \sim \mathcal{N}(0, K_z^{(n)})$
- $X_i$:输入信号
- $Y_i$:输出信号
- $Z_i$:高斯噪声,$Z_i \sim \mathcal{N}(0, K_z^{(n)})$
- 反馈不会增加离散无记忆信道的容量
- 但如果信道有记忆,反馈会增加容量
- 记带反馈信道的容量为 $C_{n,FB}$,则有:
- $C_{n,FB} \leq C_n + \frac{1}{2} \quad (\text{bit/传输})$
- $C_{n,FB} \leq 2C_n \quad (\text{bit/传输})$
- $C_n = \max_{\substack{\text{tr}(K_x) \leq nP}} \frac{1}{2n} \log \frac{|K_x + K_z|}{|K_z|}$
- $C_{n,FB} = \max_{\substack{\text{tr}(K_x) \leq nP}} \frac{1}{2n} \log \frac{|K_x + K_z|}{|K_z|}$
- 反馈可以增加信道容量,但增量不会超过 $\frac{1}{2}$ bit/传输, 也不会超过原始信道的两倍