信息论学习笔记（七）

发表于 分类于

前段时间查文献的时候，偶然看到了一些算法里涉及到了信息论的相关知识。信息论我在几年前通过看书自学过，时间太久有些忘了，正好趁此机会重新复习一下。

参考书籍：机械工业《信息论基础（原书第二版）》（ELEMENTS OF INFORMATION THEORY SECOND EDITION），作者Thomas M. Cover, Joy A. Thomas

信道容量

定义： 在 $n$ 次使用信道下，将计算出可区分信号的最大数目，这个数目与 $n$ 成指数增长关系，其对数增长率称为 信道容量 $C$。

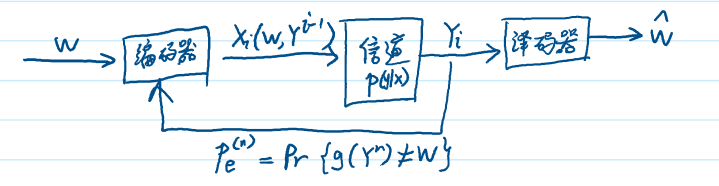
一个关于信道的模型如下图所示：

image.png

离散无记忆信道（DMC）： 由输入字母表 $\mathcal{X}$、输出字母表 $\mathcal{Y}$、概率转移矩阵 $p(y|x)$ 构成的系统。若输出的概率分布仅依赖于对应的输入，而与先前的输入或输出条件独立，则称该信道为 无记忆的。

信道容量 $C$ 的一般表达式：

$$
C = \max_{p(x)} I(X; Y)
$$

其中 $I(X; Y)$ 是输入 $X$ 和输出 $Y$ 的互信息。

典型信道类型及容量分析

如下图所示

image.png

对称信道

定义： 若信道转移矩阵 $p(y|x)$ 的任何两行可互相置换，任何两列也可互相置换，则称该信道为 对称的（symmetric）。

例子：

$$
p(y|x) = \begin{bmatrix}
0.3 & 0.2 & 0.5 \\
0.5 & 0.3 & 0.2 \\
0.2 & 0.5 & 0.3
\end{bmatrix}
$$

  • 其中第 $x$ 行 $y$ 列元素表示传输 $x$ 收到 $y$ 的概率。
  • 每一行的概率分布可通过其他行的置换得到，每一列亦然。

另一个对称信道的例子：$Y = X + Z \mod c$，其中 $Z$ 服从整数集 ${0, 1, \ldots, c-1}$ 上的某个分布，$X$ 与 $Z$ 独立，且 $X$ 与 $Z$ 具有相同的字母表。

信道容量的显式表达式： $I(X;Y)=H(Y)-H(Y|X)=H(Y)-H(r)\leq log|\mathcal{Y}|-H(r)$ 。

弱对称信道（Weakly Symmetric Channel）

若信道转移矩阵 $p(y|x)$ 的每一行都是其他行的置换，且所有列的元素之和 $\sum_xp(y|x)$ 相等，则称该信道为 弱对称的。

例子：

$$
p(y|x) = \begin{bmatrix}
\frac{1}{3} & \frac{1}{6} & \frac{1}{2} \\
\frac{1}{3} & \frac{1}{2} & \frac{1}{6} \\
\frac{1}{3} & \frac{1}{6} & \frac{1}{2}
\end{bmatrix}
$$

$\Rightarrow$ 此信道是对称的，但非严格对称。

对称信道的信道容量

对于对称信道，信道容量 $C$ 可显式表达为：

$$
C = \log |\mathcal{Y}| - H(r)
$$

  • 其中 $r$ 为转移矩阵的行。
  • 当输入字母表为均匀分布时，容量达到最大值。

信道容量的性质

  1. 非负性：由于 $I(X; Y) \geq 0$，故 $C \geq 0$。

  2. 上界：

    $$
    C = \max_{p(x)} I(X; Y) \leq \max_{p(x)} H(Y) \leq \log |Y|
    $$

    $\Rightarrow$ 容量不超过输出字母表大小的对数。

  3. 单调性：若 $|Y| \leq |X|$，则 $C \leq \log |Y|$。

  4. 连续性：互信息 $I(X; Y)$ 是关于输入分布 $p(x)$ 的连续函数。

  5. 凹凸性： 互信息 $I(X; Y)$ 是关于输入分布 $p(x)$ 的凹函数，即局部最大等于全局最大。

一些定义

  1. 用 $(X, p(y|x), Y)$ 表示的离散信道由两个有限集 $\mathcal{X}$ 与 $\mathcal{Y}$ 及一簇概率密度函数 $p(y|x) (x \in X)$ 构成。对 $\forall x \in X$ 和 $\forall y \in Y$, $p(y|x) \geq 0$. 且 $\forall x$, 有 $\sum_{y} p(y|x) = 1$. $X$ 与 $Y$ 分别看作信道的输入与输出。
  2. 离散无记忆信道 (DMC) 的 n 次扩展指信道 $(X^n, p(y^n|x^n), Y^n)$ ，其中 $p(y_k|x^k, y^{k-1}) = p(y_k|x_k), k=1,2,\cdots,n$. 若信道输入符号不依赖于过去的输出符号（即信道不带反馈），上式可简记为 $p(y^n|x^n) = \prod_{i=1}^{n} p(y_i|x_i)$
  3. 信道 $(X, p(y|x), Y)$ 的 $(M, n)$ 码由以下部分构成：
    • (1) 下标集 ${1, 2, \cdots, M}$
    • (2) 编码函数 $X^n: {1, 2, \cdots, M} \rightarrow X^n$, 上述码字 $x^n(1), x^n(2), \cdots, x^n(M)$. 其中，所有码字的集合叫码簿 (code book)
    • (3) 解码函数 $g: Y^n \rightarrow {1, 2, \cdots, M}$
  4. 条件误差概率 $\lambda_i = P_r(g(Y^n) \neq i | X^n = x^n(i)) = \sum_{y^n} p(y^n|x^n(i)) I(g(y^n) \neq i)$ ，其中 $I(*)$ 为指示性函数
  5. $(M, n)$ 码的最大误差概率：$\lambda^{(n)} = \max_{i \in {1, 2, \cdots, M}} \lambda_i$ 。算术平均误差概率 $P_e^{(n)} = \frac{1}{M} \sum_{i=1}^{M} \lambda_i$ ， 码率 $R = \frac{\log M}{n}$ (bit/传输)
  6. 若存在一个 $(\lceil 2^{nR} \rceil, n)$ 码序列，当 $n \rightarrow \infty$ 最大误差概率 $\lambda^{(n)} \rightarrow 0$ ， 则称码率 R 是可达的 (achievable) 。为简化记号，这样的序列以 $(2^{nR}, n)$ 表示
  7. 信道容量定义为 所有可达码率的上确界

联合典型序列

服从分布 $p(x,y)$ 的联合典型序列 ${(x^n, y^n)}$ 所构成的集合 $A_\varepsilon^{(n)}$ 是指其经验熵与真实熵 $\varepsilon$ 接近的 $n$ 长序列构成的集合。

$$
A_\varepsilon^{(n)} = {(x^n, y^n)} \in \mathcal{X}^n \times \mathcal{Y}^n
$$

其中

  • $|-\frac{1}{n} \log p(x^n) - H(X)| < \varepsilon$
  • $|-\frac{1}{n} \log p(y^n) - H(Y)| < \varepsilon$
  • $|-\frac{1}{n} \log p(x^n, y^n) - H(X,Y)| < \varepsilon$

其中 $p(x^n, y^n) = \prod_{i=1}^n p(x_i, y_i)$

若 $(X^n, Y^n)$ 为服从 $p(x^n, y^n) = \prod_{i=1}^n p(x_i, y_i)$ 的 i.i.d. 的 $n$ 长序列，那么：

  1. 当 $n \to \infty$, $Pr((X^n, Y^n) \in A_\varepsilon^{(n)}) \to 1$
  2. $|A_\varepsilon^{(n)}| \leq 2^{n(H(X,Y)+\varepsilon)}$
  3. 如果 $(\hat{X}^n, \hat{Y}^n) \sim p(x^n)p(y^n) \Rightarrow \hat{X}^n$ 与 $\hat{Y}^n$ 独立，且与 $p(x^n, y^n)$ 有相同的边缘分布，则 $Pr((\hat{X}^n, \hat{Y}^n) \in A_\varepsilon^{(n)}) \leq 2^{-n(I(X;Y)-3\varepsilon)}$

且对于充分大的 $n$, $Pr((\hat{X}^n, \hat{Y}^n) \in A_\varepsilon^{(n)}) \geq (1-\varepsilon)2^{-n(I(X;Y)+3\varepsilon)}$

信道编码定理（信道容量的可达性）

  • 对于离散无记忆信道，小于信道容量 $C$ 的所有码率都是可达的。
  • 具体来说，对任意码率 $R < C$，存在一个 $(2^{nR}, n)$ 码序列，它的最大误码概率为 $\lambda^{(n)} \to 0$
  • 反之，任何满足 $\lambda^{(n)} \to 0$ 的 $(2^{nR}, n)$ 码序列必有 $R \leq C$。

带反馈的信道容量

  • 离散无记忆信道的带反馈容量 $C_{FB}$ 定义为反馈码可以达到的所有码率的上确界。

image.png

反馈容量：$C_{FB} = C = \max_{p(x^n)} I(X;Y)$

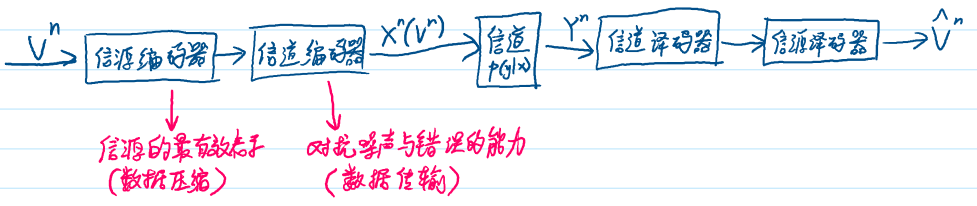
信源信道分离定理

  • 若 $V_1, V_2, \cdots, V_n$ 为有限字母表上满足 渐进均分性（AEP） 和 $H(V) < C$ 的随机过程，则存在一个信源信道编码使得误差概率 $Pr(\hat{V}^n \neq V^n) \to 0$。反之，若 $H(V) > C$，则误差概率趋于 0。

image.png