信息论学习笔记（五）

发表于 更新于 分类于

前段时间查文献的时候，偶然看到了一些算法里涉及到了信息论的相关知识。信息论我在几年前通过看书自学过，时间太久有些忘了，正好趁此机会重新复习一下。

参考书籍：机械工业《信息论基础（原书第二版）》（ELEMENTS OF INFORMATION THEORY SECOND EDITION），作者Thomas M. Cover, Joy A. Thomas

信息论笔记 - 信源编码与数据压缩

信源编码 $C$

  • 定义：从随机变量 $X$ 的取值空间到 $D^*$ 的一个映射。

    • $D^*$ 表示字母表 $\mathcal{D}$ 上的有限长度字符串构成的集合。
    • $C(x)$ 表示 $x$ 的码字，$l(x)$ 表示 $C(x)$ 的长度。
    • 示例：若 $X = {\text{红}, \text{蓝}}$，则 $C(\text{红}) = 00$，$C(\text{蓝}) = 11$，这是基于字母表 $D = {0, 1}$ 的信源编码。

      期望长度 $L(C)$

  • 定义：设随机变量 $X$ 的概率密度函数为 $p(x)$，则定义信源编码 $C(X)$ 的期望长度 $L(C)$ 为：
    $$
    L(C) = \sum_{x \in X} p(x) l(x)
    $$

    • 其中， $l(x)$ 对应于 $x$ 的码字长度。

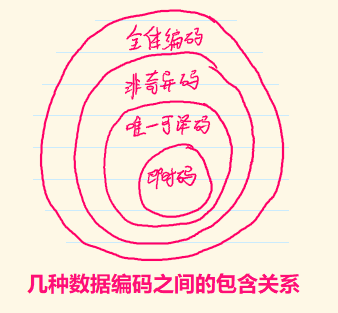
非奇异编码

  • 定义：若编码将 $X$ 的每个元素映射到 $D^*$ 中不同的字符串，即 $x \neq x’ \Leftrightarrow C(x) \neq C(x’)$，则称该编码为 非奇异编码。

  • 扩展编码 $C^*$：将 $X^n$ 映射到 $D^*$ 的有限长度字符串的映射，定义为 $C(x_1, x_2, \ldots, x_n) = C(x_1)C(x_2)\cdots C(x_n)$ ，即相应码字的串联。示例：若 $C(\text{红}) = 00$，$C(\text{蓝}) = 11$，则 $C(\text{红}, \text{蓝}) = 0011$。

    • 若编码 $C$ 的扩展编码 $C^*$ 是非奇异的，则称 $C$ 是 唯一可译的。

      即时码（instantaneous code），或称前缀码（prefix code）

  • 定义：码中无任何码字是其他码字的前缀。

    • 这是一种“自我中断码”，无需参考后面的码字即可解码。
    • 示例：
1
2
3
4
5
6
7
8
9
编码方案：
	C(1)=0
	C(2)=10
	C(3)=110
	C(4)=111
则对于二元串 01011111010
可以分解为:
	0,10,111,110,10
	1, 2,  4,  3, 2

image.png

Kraft 不等式

  • 基本形式：对于字母表 $D$ 上的即时码（前缀码），码字长度 $l_1, l_2, \ldots, l_m$ 必须满足：

$$
\sum_{i=1}^m D^{-l_i} \leq 1
$$

  • 反之，给定一组满足上述不等式的码字长度 $l_1, l_2, \ldots, l_m$，则存在一个对应的即时码，其码字长度即为给定的长度。
  • 推广形式：对任意构成前缀码的可数无限码字集，码字长度满足推广的 Kraft 不等式：
    $$
    \sum_{i=1}^\infty D^{-l_i} \leq 1
    $$

image.png

最优码：求解前缀码的最小化期望长度问题

  • 目标：求解满足 Kraft 不等式的长度集合 $l_1, l_2, \ldots, l_m$，使期望长度 $L = \sum p_i l_i$ （约束条件 $\sum{D^{-li}}\le 1$ ）不超过其他前缀码的 $L$。
  • 经推导，最优码长：$l_i^* = -\log_D p_i$
  • 期望码字长： $L^* = \sum p_i l_i^* = -\sum p_i \log_D p_i = H_D(X)$
  • 由于 $l_i$ 必须是整数， $l_i$ 应该尽可能接近 $-log_D p_i$
  • 随机变量 $X$ 的任一 $D$ 元前缀码的期望长度 $L \geq H_D(X)$，当且仅当 $D^{-l_i} = p_i$ 取等号。

概率分布与编码效率

  • 均匀分布情况：若某个 $n$，概率分布的每个概率值均等于 $D^{-n}$，则该概率分布是 $D$-进制的（$D$-adic）。
  • 一般情况：期望描述长度 $L$ 的取值范围为 $H(X) \leq L < H(X) + 1$。

随机过程的熵率

  • 定义 $L_n$ 为每输入 $n$ 字母的期望码字长度：

$$
L_n = \frac{1}{n} \sum p(x_1, x_2, \ldots, x_n) l(x_1, x_2, \ldots, x_n)=\frac{1}{n}El(x_1,x_2,\ldots,x_n)
$$

  • 则：

$$
\frac{H(X_1, X_2, \ldots, X_n)}{n} \leq L_n^* < \frac{H(X_1, X_2, \ldots, X_n)}{n} + \frac{1}{n}
$$

  • 若 $X_1, X_2, \ldots, X_n$ 为平稳随机过程，则 $L_n^* \to H(X)$ ，后者为随机过程的熵率。

编码定理

  • 错码定理：对于任意编码，若码字长度分配 $l(x) = \lceil \log \frac{1}{p(x)} \rceil$，则关于 $p(x)$ 的期望码长满足：
    $$
    H(p) + D(p | q) \leq E_p[l(x)] < H(p) + D(p | q) + 1
    $$
    • 其中 $D(p | q)$ 为相对熵。

McMillan 定理

  • 唯一可译码的必要条件：任何唯一可译的 $D$-元码的码字长度必须满足 Kraft 不等式：
    $$
    \sum D^{-l_i} \leq 1
    $$

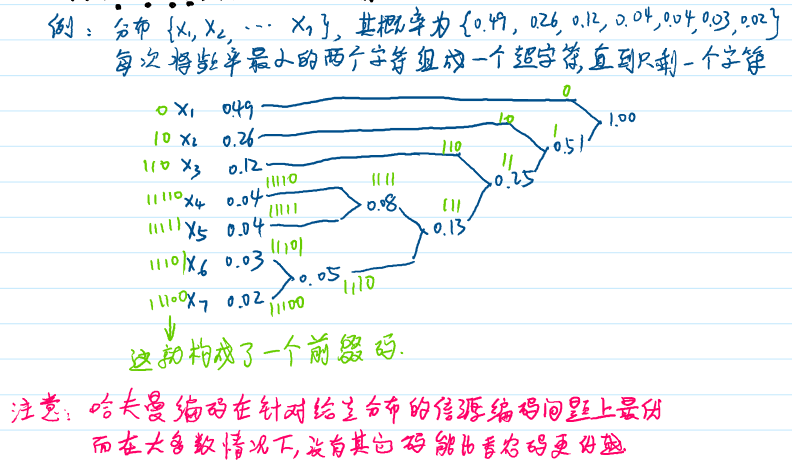
哈夫曼码

  • 定义：给定概率分布，构造最优的前缀码。
  • 构造方法：每次合并概率最小的两个字符形成一个超字符，直到只剩一个字符。

image.png

哈夫曼码的最优性

引理 5.8.1：

对于任意给定分布，存在满足如下性质的一个最优即时码：

  1. 长度序列与概率分布排列顺序相反：若 $p_j > p_k$，则 $l_j \leq l_k$。
  2. 最长的两个码字具有相同长度。
  3. 最长的两个码字仅在最后一位有所差别，对应于最小可能的两个字符。

满足这些性质的最优码称为 **典则码 (canonical code)**。

哈夫曼码的最优性

  • 若 $C^*$ 是哈夫曼码，$C’$ 是其他码，则 $L(C^*) \leq L(C’)$。

通过均匀硬币投掷生成离散分布

  • 对任意完全树，考虑所有叶子上的概率分布，使得深度为 $k$ 的每片叶子的概率为 $2^{-k}$，则树的期望深度 $E(T)$ 等于该分布的熵：

$$
E(T) = H(Y)
$$

  • $\mathcal{Y}$ 为一棵完全树的叶子，$Y$ 为 $\mathcal{Y}$ 的取值集合（？）。

生成随机变量的期望代价

  • 对任何生成 $X$ 的算法，$E(T) \geq H(X)$。
  • 若 $X$ 服从二进制分布，则由抛硬币生成 $X$ 的最优算法的期望抛掷次数 $E(T) = H(X)$。
  • 若 $X$ 不是二进制分布，则 $H(X) \leq E(T) \leq H(X) + 2$。

$\Rightarrow$ 平均抛硬币 $H(X) + 2$ 次即可模拟随机变量 $X$。