相关性系数与线性回归

发表于 分类于

第五次生物统计学助教课的备课笔记。

本文为生统助教课备课过程的一些记录，主要涉及相关性系数、一元线性回归、多元线性回归等知识点。

一张图展示本文知识大纲：

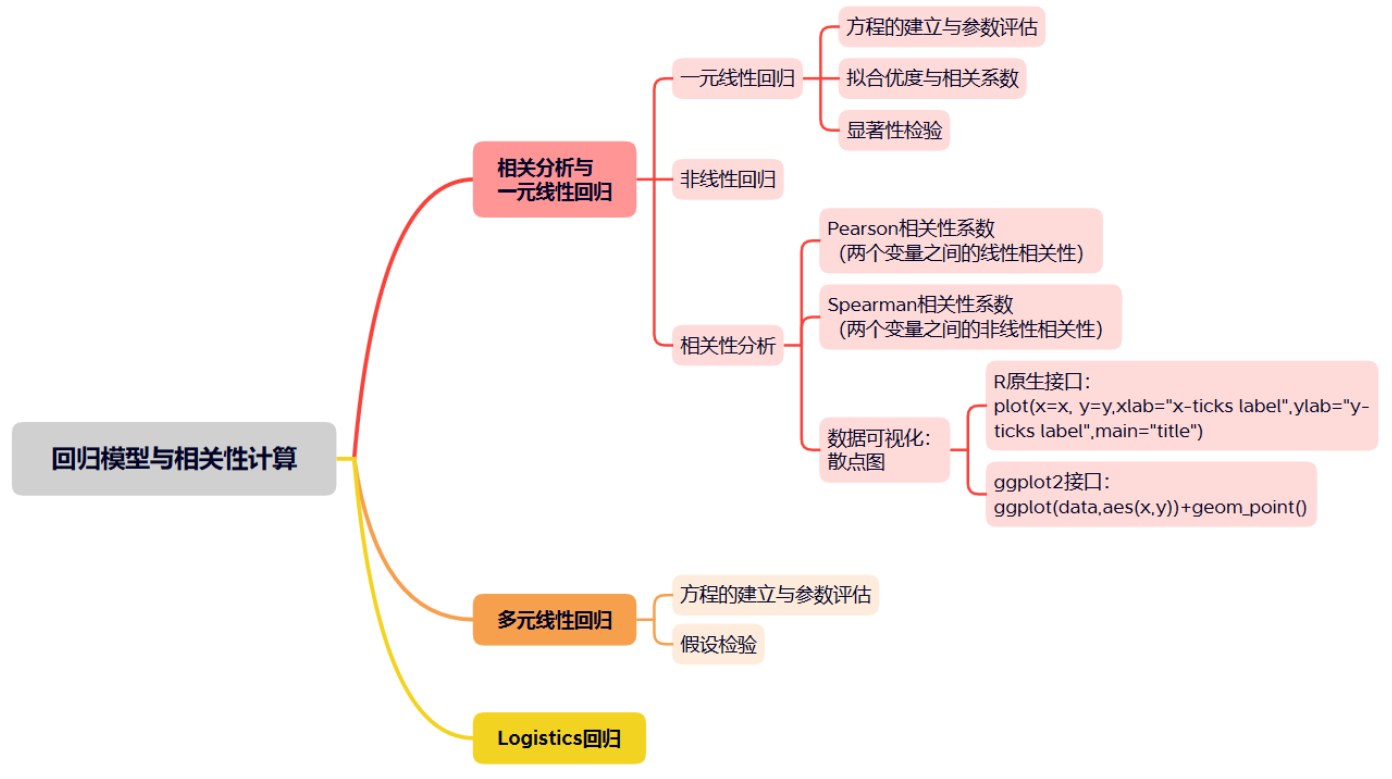
image.png

一、一元线性回归与相关性系数

（一）一元线性回归

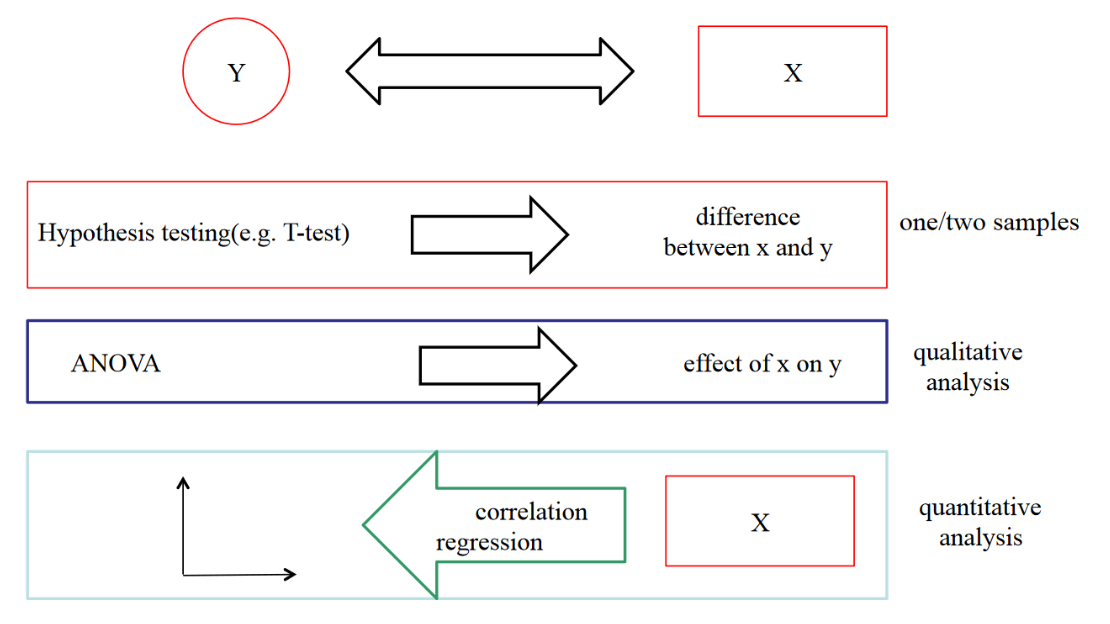
上一次助教课我们回顾了ANOVA的数学原理，其用来对多组数据的均值差异做检验。线性回归相当于是对ANOVA的进一步拓展，当分组数量是一个连续型变量时，如何检验均值差异的显著性，如何确定自变量（实验因子）对响应变量的影响，就是一元线性回归要解决的问题了。

image.png

最小二乘法

使用最小二乘法推导线性回归的公式：

image.png

另外，还有几个很有用的变量，在线性回归和相关性分析中会被用到： $L_{xx},L_{yy},L_{xy}$ ，这三个变量反映了自变量x、因变量y的误差平方和，以及x与y的交叉项的误差平方和，它们的计算公式如下图所示：

image.png

R语言中，线性回归的函数接口是 lm(formula,data) ，其既可以做一元线性回归，又可以做多元线性回归。

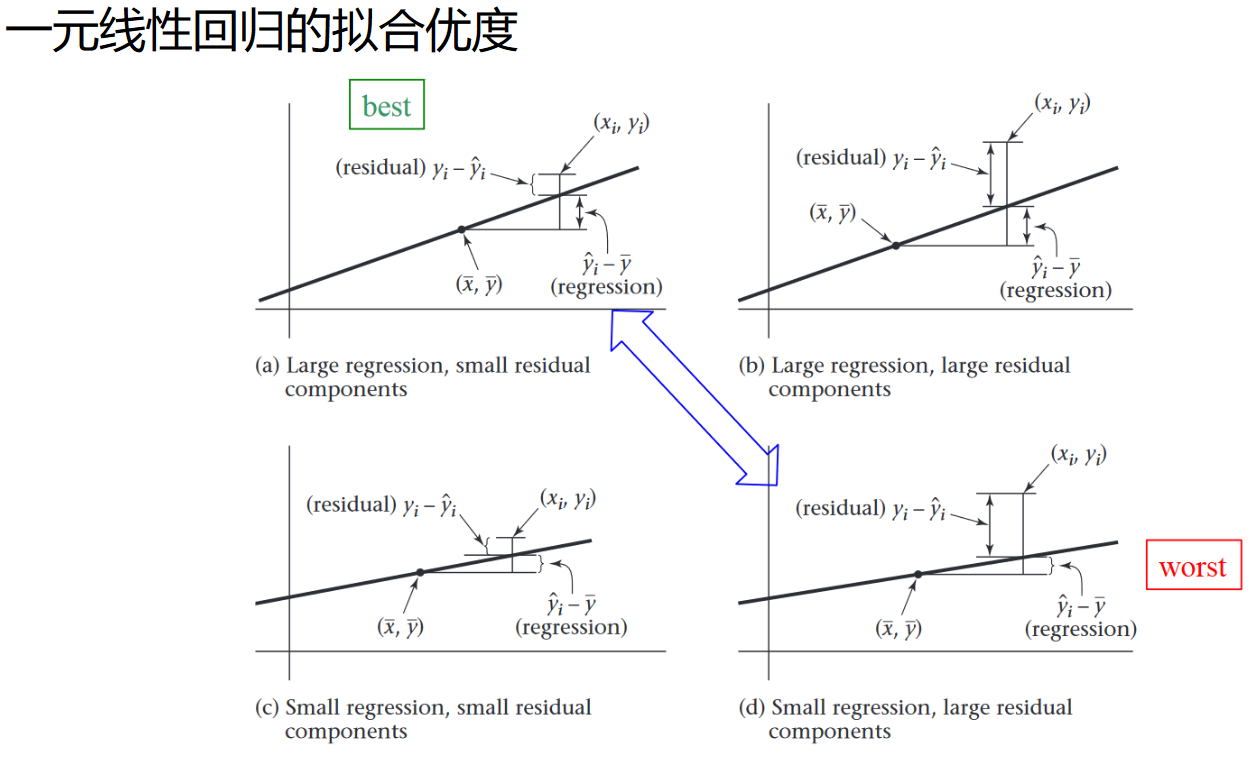
拟合优度

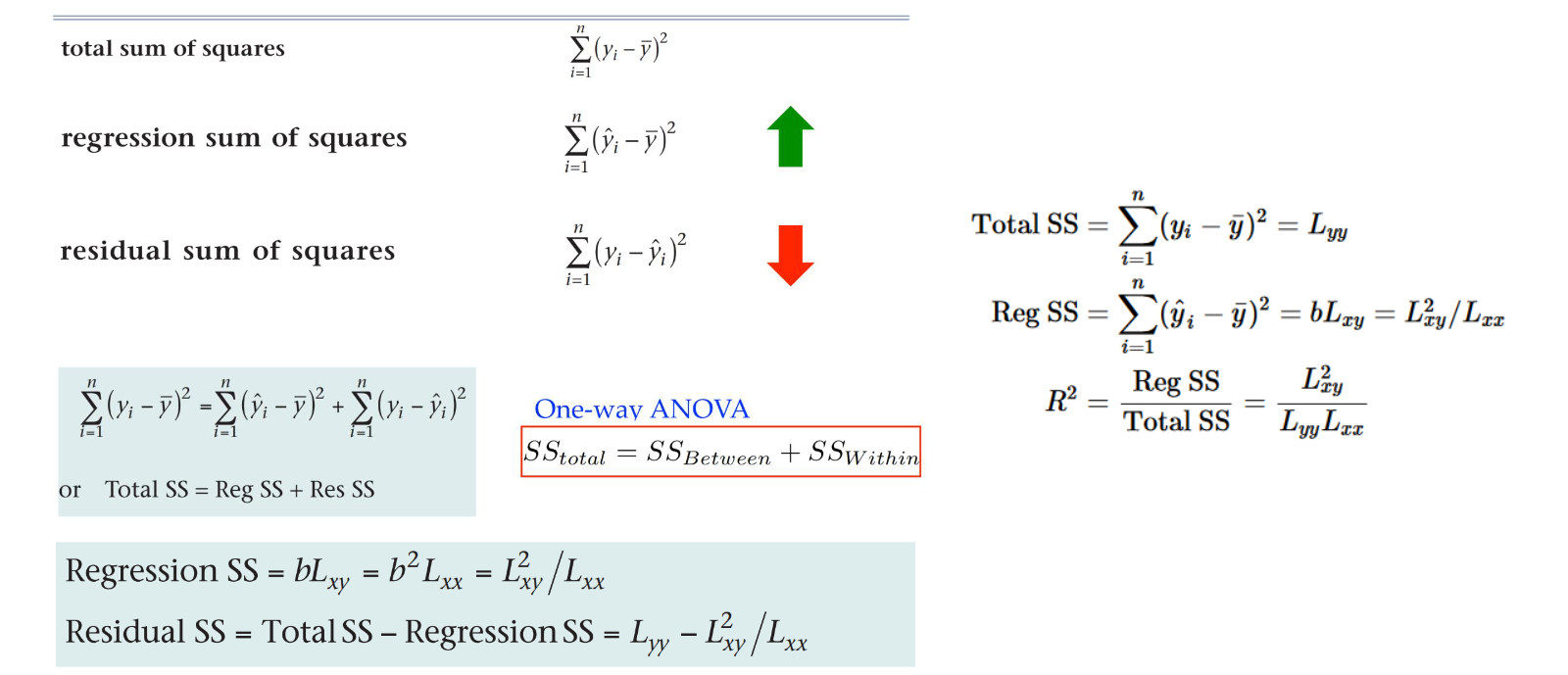
拟合优度是一个判断线性回归好与坏的指标，其衡量了回归模型对变量方差的解释程度（RegSS）在变量的总方差（TotalSS）中的占比， 其计算公式（ $R^2$ ）如下：

image.png

image.png

一元线性回归的F检验和t检验

F检验看的是所有自变量对因变量的解释程度，其原理类似ANOVA的F检验。

image.png

t检验看的是单个自变量对模型因变量的解释程度。对于一元线性回归来说，t检验和F检验是等价的检验过程；但是对于多元回归模型来说，F检验看的是一整个模型的显著性，而t检验看的就是每个自变量各自的显著性了。

image.png

（二）相关性系数

常用的相关性系数有两个：Pearson相关性系数（检验变量之间的线性相关性）和Spearman相关性系数（检验非线性的相关性）

Pearson相关性系数

Pearson相关性系数的定义有两个，分别是基于协方差的定义与基于一元线性回归方程 $R^2$ 的定义。注意存在关系式 $r=\sqrt{R^2}$ 。Pearson相关性系数的取值范围是 [-1,1] ，当r=-1时代表显著的负相关，r=1代表显著的正相关。

image.png

Spearman相关性系数

Spearman 相关系数衡量的是两列数据的排名之间的线性关系，其先将两组数据的值分别转换为各自的秩次排名（rank），然后对rank做Pearson相关性系数的计算。另外，存在一个简化公式 $\rho=1-\frac{6\sum{d_i^2}}{n(n^2-1)}$ ，在数据中没有秩次并列（“结”，tied ranks）时可以用于简化计算。

image.png

二、多元线性回归

最小二乘法公式推导：

image.png

显著性检验（F检验）：

image.png

另外，R语言中有函数接口 anova() 可以用来比较两个线性回归模型。下面以R语言内置数据集 BreastCancer 为例，展示模型比较的过程：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
df3.omit <- na.omit(BreastCancer)
# 第一个模型，使用全部自变量建模
fit3.full <- glm(response~Cl.thickness+Cell.size+Cell.shape+
                   Marg.adhesion+Epith.c.size+Bare.nuclei+
                   Bl.cromatin+Normal.nucleoli+Mitoses,
                data=df3.omit,
                family=binomial(link="logit"),
                control=list(maxit=100))
# 第二个模型，使用部分t检验显著的自变量建模
fit3.reduced <- glm(response~Cl.thickness+Marg.adhesion+Bare.nuclei+
                      Bl.cromatin+Normal.nucleoli,
                data=df3.omit,
                family=binomial(link="logit"),
                control=list(maxit=100))
# 建模结果比较（卡方检验）
anova(fit3.full,fit3.reduced,test="Chisq")

output:

1
2
3
4
5
6
7
8
9
10
11
12
## Analysis of Deviance Table
## 
## Model 1: response ~ Cl.thickness + Cell.size + Cell.shape + Marg.adhesion + 
##     Epith.c.size + Bare.nuclei + Bl.cromatin + Normal.nucleoli + 
##     Mitoses
## Model 2: response ~ Cl.thickness + Marg.adhesion + Bare.nuclei + Bl.cromatin + 
##     Normal.nucleoli
##   Resid. Df Resid. Dev Df Deviance Pr(>Chi)  
## 1       673     102.90                       
## 2       677     112.26 -4  -9.3637  0.05262 .
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

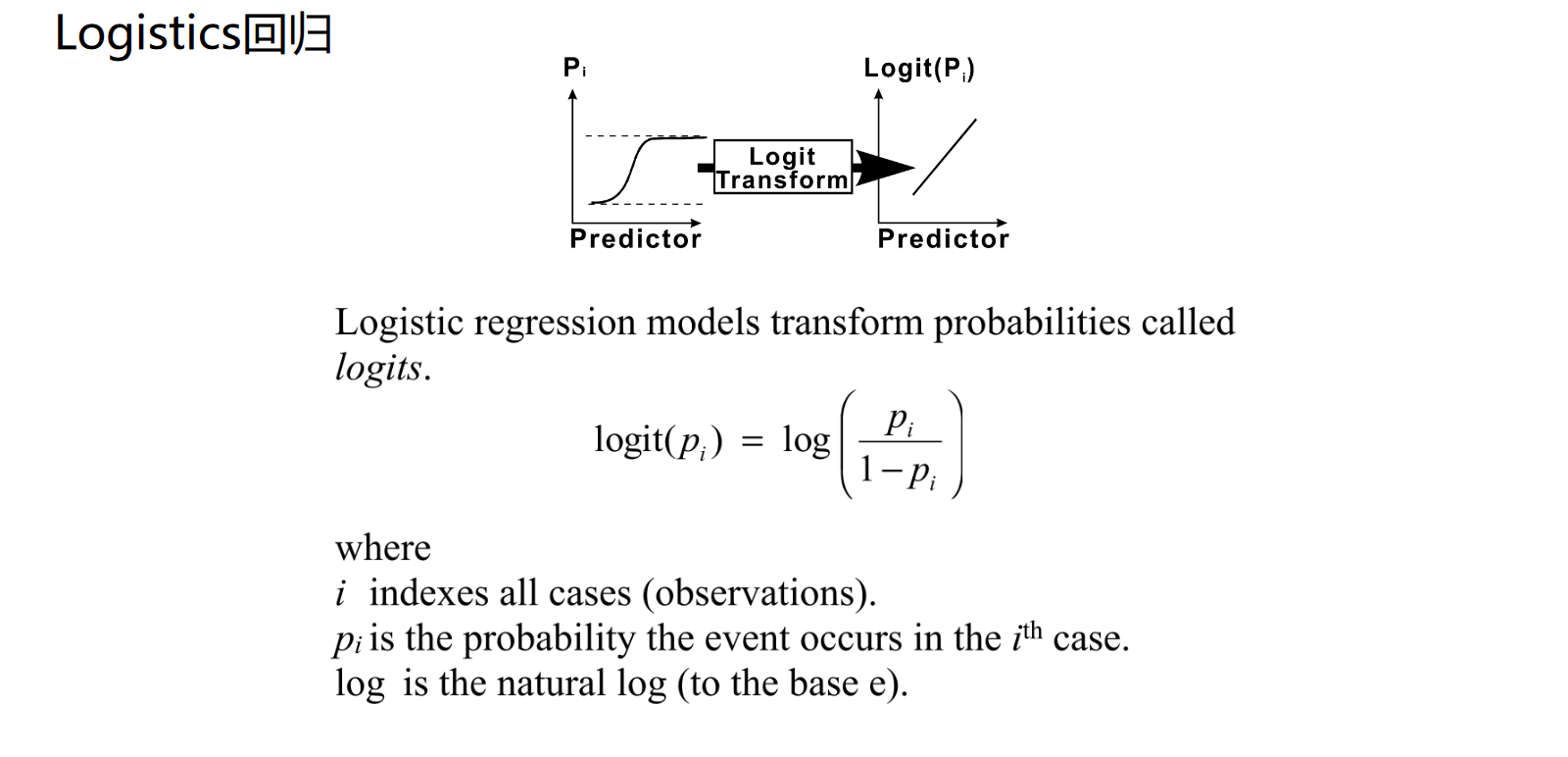
非线性回归与逻辑回归

非线性回归：使用一些函数变换，可以将模型变为线性回归。

image.png

逻辑回归：其使用 logit() 函数进行变换，值域为 (0,1) ，常用于机器学习模型的激活函数当中。

image.png