信息论学习笔记(二)
前段时间查文献的时候,偶然看到了一些算法里涉及到了信息论的相关知识。信息论我在几年前通过看书自学过,时间太久有些忘了,正好趁此机会重新复习一下。
参考书籍:机械工业《信息论基础(原书第二版)》(ELEMENTS OF INFORMATION THEORY SECOND EDITION),作者Thomas M. Cover, Joy A. Thomas
基本概念
离散型随机变量的熵
设 $X$ 是一个离散型随机变量,其字母表(取值空间)为 $\mathcal{X}$,概率质量函数为 $p(x) = \Pr(X = x), x \in \mathcal{X}$。
熵的定义
熵 $H(X)$ 表示随机变量 $X$ 的不确定性程度,定义为:
$$
H(X) = -\sum_{x \in \mathcal{X}} p(x) \log_2 p(x)
$$
- $H(X)$ 可以解释为 $\text{log}\frac{1}{p(x)}$ 的期望,因此 $H(X)=E_p\text{log}\frac{1}{p(x)}$ 。
- 单位: 比特(bit)
- 约定: $0 \log 0 = 0$
- 记法: 有时简记为 $H(p)$
- 当对数底数为自然常数 $e$ 时,熵的单位为 奈特(nat)。
- 熵的非负性:$H(X) \geq 0$。
- 换底公式: $H_b(X)=(\text{log}ba)H_a(X)$ , $H_b(X)=-\sum{x\in \mathcal{X}}p(x)\text{log}_bp(x)$
注意: 熵仅依赖于 $X$ 的概率分布,与具体取值无关。
联合熵与条件熵
联合熵
对于一对离散随机变量 $(X, Y)$,其联合熵定义为:
$$
H(X, Y) = -\sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} p(x, y) \log p(x, y)
$$
等价形式:
$$
H(X, Y) = -E[\log p(X, Y)]
$$
条件熵
条件熵 $H(Y|X)$ 表示已知 $X$ 后 $Y$ 的剩余不确定性:
$$
\begin{aligned}
H(Y|X) &= \sum_{x \in \mathcal{X}} p(x) H(Y|X = x) \\
&= -\sum_{x \in \mathcal{X}} p(x) \sum_{y \in \mathcal{Y}} p(y|x) \log p(y|x) \\
&= -\sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} p(x, y) \log p(y|x) \\
&= -E[\log p(Y|X)]
\end{aligned}
$$
链式法则
联合熵与条件熵满足链式关系:
$$
H(X, Y) = H(X) + H(Y|X)
$$
推广到多个变量时:
$$
H(X, Y|Z) = H(X|Z) + H(Y|X, Z)
$$
此外,虽然条件熵的交换律 $H(Y|X)=H(X|Y)$ 不成立 ,但是下面的交换律是 成立 的:
$$
H(X)-H(X|Y)=H(Y)-H(Y|X)
$$
相对熵(KL散度)
定义
相对熵(Kullback-Leibler divergence)衡量两个概率分布 $p$ 和 $q$ 的差异程度:
$$
D(p \parallel q) = \sum_{x \in \mathcal{X}} p(x) \log \frac{p(x)}{q(x)} = E_p \left[ \log \frac{p(X)}{q(X)} \right]
$$
- 约定:$0 \log \frac{0}{0} = 0$,$0 \log \frac{0}{q} = 0$,$p \log \frac{p}{0} = \infty$
- 性质:
- $D(p \parallel q) \geq 0$,当且仅当 $p = q$ 时取等号。
- 非对称性:$D(p \parallel q) \neq D(q \parallel p)$。
- 不满足三角不等式,因此不是严格意义上的距离。
互信息
定义
互信息 $I(X; Y)$ 表示随机变量 $X$ 和 $Y$ 之间的相关性:
$$
\begin{aligned}
I(X; Y) &= \sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} p(x, y) \log \frac{p(x, y)}{p(x)p(y)} \\
&= D(p(x, y) \parallel p(x)p(y)) \\
&= E_{p(x,y)} \left[ \log \frac{p(X,Y)}{p(X)p(Y)} \right]
\end{aligned}
$$
- 几何意义:一个随机变量包含另一个随机变量的信息量。
- 等价形式:
$$
I(X; Y) = H(X) - H(X|Y) = H(Y) - H(Y|X) = H(X)+H(Y)-H(X,Y)
$$
$$
I(X; X) = H(X) \quad (\text{自信息})
$$
韦恩图示意
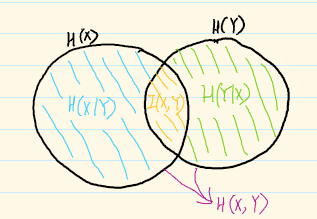
熵的链式法则
对于多个随机变量 $X_1, X_2, \ldots, X_n$:
$$
H(X_1, X_2, \ldots, X_n) = \sum_{i=1}^n H(X_i | X_{i-1}, \ldots, X_1)
$$
条件互信息
定义
给定第三个随机变量 $Z$ 。在 $Z$ 条件下, $X$ 与 $Y$ 的互信息即为条件互信息,其定义为:
$$
\begin{aligned}
I(X; Y | Z) &= H(X | Z) - H(X | Y, Z) \
&= E_{p(x,y,z)} \left[ \log \frac{p(x,y|z)}{p(x|z)p(y|z)} \right]
\end{aligned}
$$
- 链式法则:
$$
I(X_1, X_2, \ldots, X_n; Y) = \sum_{i=1}^n I(X_i; Y | X_{i-1}, \ldots, X_1)
$$
熵与相对熵的凸性
Jensen不等式
- 给定一个函数 $f$ 和随机变量 $X$ ,若 $f$ 是凸函数,则:$E[f(X)] \geq f(E[X])$
- 反之,若 $f$ 是凹函数,则:$E[f(X)] \leq f(E[X])$
- 相对熵的凸性:
$$
D(\lambda p_1 + (1-\lambda) p_2 \parallel \lambda q_1 + (1-\lambda) q_2) \leq \lambda D(p_1 \parallel q_1) + (1-\lambda) D(p_2 \parallel q_2)
$$ - 熵的凹性:$H(p)$ 是关于 $p$ 的凹函数。
- 均匀分布的元素熵最大: $H(X) \leq \text{log} |\mathcal{X}|$ ,当且仅当 $X$ 服从 $\mathcal{X}$ 上的均匀分布时等号成立。
- 信息不会有副作用: $H(X|Y) \leq H(X)$ ,如果已经有 $Y$ 提供了一些信息,那么此时再有 $X$ 提供信息,那么 $X$ 所能提供的信息量(条件熵)要小于 $X$ 自身单独能够提供的所有信息。当且仅当 $X$ 与 $Y$ 互相独立时等号成立。
数据处理不等式
若存在马尔可夫链 $X \rightarrow Y \rightarrow Z$,则:
$$
I(X; Y) \geq I(X; Z)
$$
- 推论:若 $\theta \rightarrow X \rightarrow T(X)$,则 $I(\theta; X) \geq I(\theta; T(X))$。
- 充分统计量:若 $T(X)$ 是关于分布族 ${p_\theta(x)}$ 的充分统计量,则其保留了样本中关于 $\theta$ 的全部信息。
费诺不等式
设 $\hat{X}$ 是基于观测 $Y$ 对 $X$ 的估计量,错误概率 $P_e = \Pr{X \neq \hat{X}}$,则:
$$
\begin{aligned}
H(P_e) + P_e \log |\mathcal{X}| &\geq H(X | \hat{X}) \\
&\geq H(X | Y) \\
\Rightarrow \quad P_e &\geq \frac{H(X | Y) - 1}{\log |\mathcal{X}|}
\end{aligned}
$$
- 推论:若 $P_e = \Pr{X \neq \hat{X}}$,且 $\hat{X}$ 由 $Y$ 生成,则:
$$
H(P_e) + P_e \log (|\mathcal{X}| - 1) \geq H(X | Y)
$$