方差分析(ANOVA)与缺失值处理
第四次生物统计学助教课的备课笔记。
本文为生统助教课备课过程的一些记录,主要涉及单因素方差分析(one-way ANOVA)、双因素方差分析(two-way ANOVA)的基本概念与计算方法,以及缺失值处理的相关知识点。
一张图展示本文知识大纲:
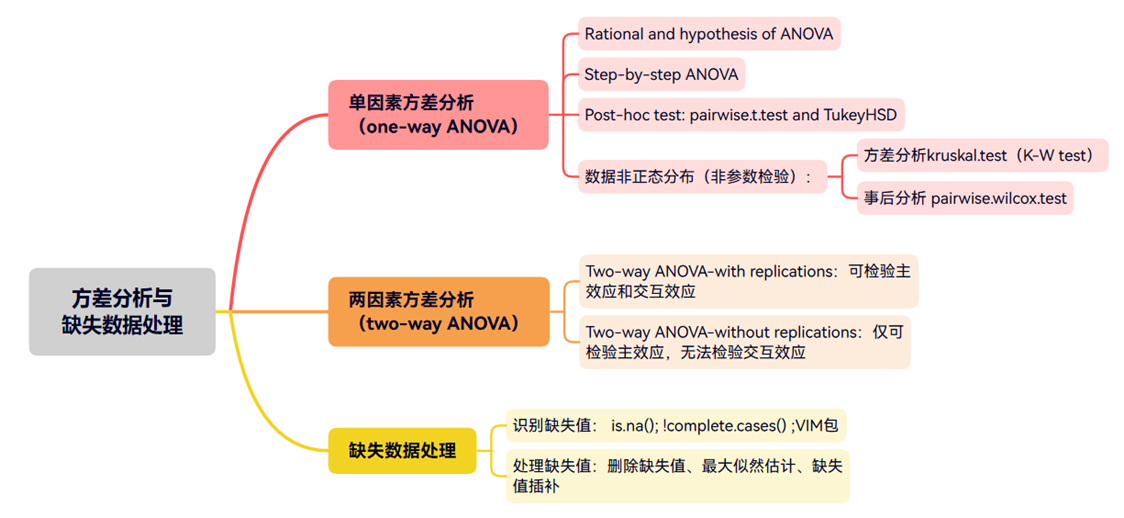
一、单因素方差分析
- ANOVA回答的问题:对多个组的平均值进行检验,判断所有组的平均值是否相同,或者至少其中一个平均值与其他组不同。
- 检验对象:多组样本所对应的群体均值是否相等,观察到的各组样本平均值之间的差异是否归因于随机抽样误差。
- ANOVA分析基本假设:样本是从正态分布群体中随机抽取的,并且相互独立,方差相等。
- ANOVA的原始假设与备择假设:
- H0: 多个样本之间的population mean相同。(观测数据中的差异是由抽样误差造成,如下图左图)
- H1: 多个样本之间的population mean中,至少有一个与其他的不同。(观测数据中的差异就是实际差异,如下图右图)
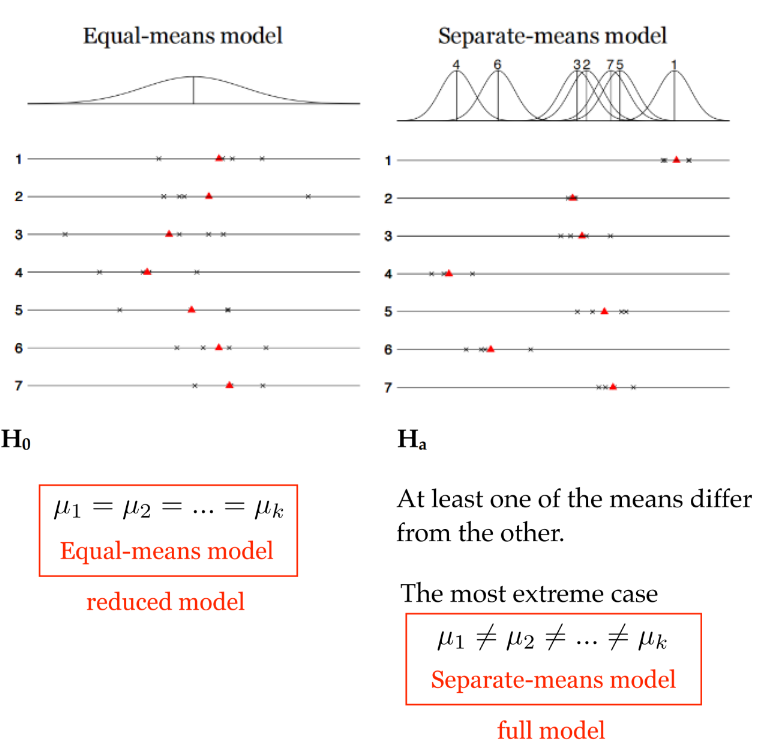
虽然我们比较的是各组之间的平均值,但是很显然组内方差和组间方差更适合我们去做这样的判断。因此,ANOVA的检验思路就是将所有样本的总方差分解为组内方差和组间方差,并进行比较(如下图)。若组间差异远小于组内差异,则认为组间均值无显著差异(接受H0);否则,拒绝H0,认为至少一组样本的均值与其他的不同(接受H1)

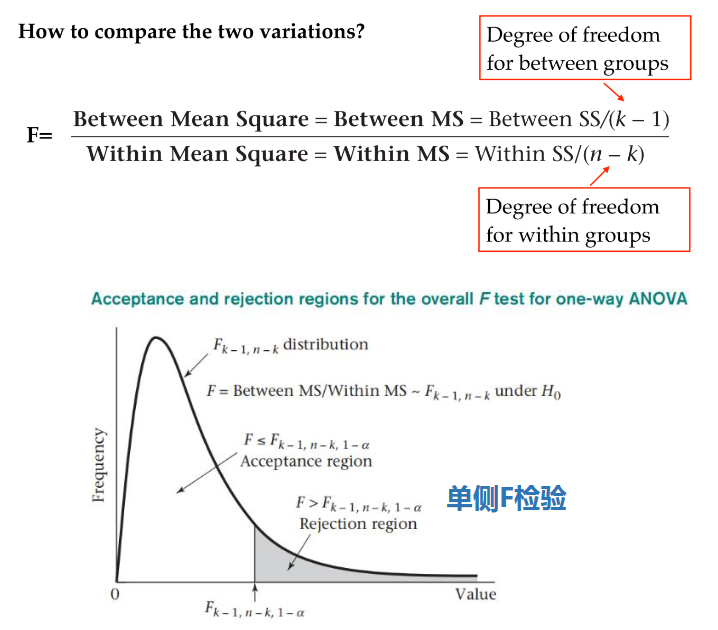
因此,ANOVA检验就是对两个不同的方差进行检验,这里涉及F检验的相关知识。如下图是F分布的相关知识点,放在这里帮助我们复习一下F检验的数学原理。

对于ANOVA来说,其检验统计量的计算方法为 $F=between MS/within MS$ , 即组间方差比上组内方差。零假设下,组间均方除以组内均方应该服从F分布。
- 若H0为真(没有组间差异),则组间方差估计量(Between MS)和组内方差估计量(Within MS)其实是同一个总体方差σ²的两种估计,各自都(在零假设下)分别服从自由度不同的卡方分布:
- 组间均方(MSBetween) $= SS_{Between}/(k-1) \sim χ^2(k-1)$
- 组内均方(MSWithin) $= SS_{Within}/(n-k) ~ χ^2(n-k)$
- 其中 $n$ 为总样本量 , $k$ 为组数。
- 二者的比值就是两自由度独立卡方分布单元归一后的比值,这正是F分布的定义。
- 因此,ANOVA的检验统计量可以使用这一公式进行计算: $F=MS_{Between}/MS_{Within} \sim F(k-1,n-k)$
- 其中 $n$ 为总样本量 , $k$ 为组数。
one-way ANOVA的检验方法(step-by-step)
如下图。

下面我们以一个具体的问题为例,展示一下如何进行ANOVA分析。如下表所示,科学家测试了四种抗生素对某种细菌的抑菌效果,每一种抗生素进行了6组平行实验,请问根据表格中的数据,是否至少有一组抗生素的抑菌效果与其他各组显著不同?
| antibiotic | data |
|---|---|
| Penicillin | 29.6 , 24.3 , 28.5 , 32 , 26.1 , 31 |
| Tetracycline | 27.3 , 32.6 , 30.8 , 34.8 , 29.4 , 33.1 |
| Erythromycin | 21.6 , 17.4 , 18.3 , 19 , 19.5 , 18 |
| Chloramphenicol | 29.2 , 32.8 , 25 , 24.2 , 26.6 , 28.9 |
首先是空假设和备择假设: H0:所有组别的抑菌效果都一样;H1:至少有一组抗生素的抑菌效果与其他各组显著不同。
首先,我们对这四组数据进行正态性检验,发现这几组数据都符合正态性的假设(过程略)。接下来,我们可以分布计算出下面的这些统计量:
| group | n | average | variance |
|---|---|---|---|
| Penicillin | 6 | 28.58333 | 8.613667 |
| Tetracycline | 6 | 31.33333 | 7.406667 |
| Erythromycin | 6 | 18.96667 | 2.210667 |
| Chloramphenicol | 6 | 27.78333 | 10.08167 |
| total | 24 | 26.66667 | 28.58667 |
我们进一步可以求出:
$$
\begin{aligned}
SS_{total} &= \sum\sum(x_{ij}-\bar{\bar x})^2 &= 657.4933 \\
SS_{between} &= \sum\sum(x_j-\bar{\bar x})^2 &= 515.9300 \\
SS_{within} &= \sum\sum(x_{ij}-\bar{x_j})^2 &= 141.5633
\end{aligned}
$$
其中,有关系式 $SS_{total}=SS_{between}+SS_{within}$ ,我们可以基于这个关系式检验我们的计算结果。
我们的数据总共有4组,因此k=4。每一组有6个平行重复,因此n=24,因此我们可以进一步求得:
$$
\begin{aligned}
df_1 &= k-1 \\
&= 3 \\
df_2 &= n-k \\
&= 20 \\
F &= \frac{SS_{between}/df_1}{SS_{within}/df_2} \\
&= \frac{515.9300/3}{141.5633/20} \\
&\approx 24.29679 \\
\end{aligned}
$$
查表得,在显著性水平 $\alpha=0.05$, 自由度 df1=3 且 df2=20 的情况下,F统计量的边界值为 $3.098 < 24.29679$ ,因此我们拒接H0,接受H1,认为至少一组抗生素的抑菌效果与其他各组显著不同(经过事后检验,我们可以发现是红霉素Erythromycin的抗菌效果显著低于另外三种抗生素)。
事后检验(Post-hoc test)
在R语言中,有两种事后检验方法的函数接口,分别是 Pairwise.t.test() 和 TukeyHSD() ,前者传入原始数据的dataframe,后者则传入 aov() 函数的返回值。

非参数检验
上面列举的one-way ANOVA检验方法,是建立在数据符合正态性假设的前提下的,如果数据不符合正态性,则需要使用非参数方法,其中R语言里提供的函数接口是 kruskal.test() ,这是一种从wilcox秩和检验发展而来的检验方法,通过检验不同分组之间的中位数是否相同而获得结果。
下图是一张总结,展示了对于多组数据的检验中,如何选择合适的检验方法,以及进行事后检验。

二、双因素方差分析
带有重复的双因素方差分析
two-way ANOVA分为带有重复的(Two-way ANOVA with replications)和不带重复的(Two-way ANOVA without replications)。二者的区别在于,带有重复的ANOVA需要考虑双因子之间的互作,而不带重复的则不需要考虑互作。
下图是one-way ANOVA与Two-way ANOVA with replications的比较。

Two-way ANOVA的数学原理也涉及对方差的分解与检验,注意这里需要计算三个检验统计量 $F_{A}$, $F_{B}$, $F_{AB}$, 分别用于检验因子A、B各自的效应,以及A与B互作的效应。
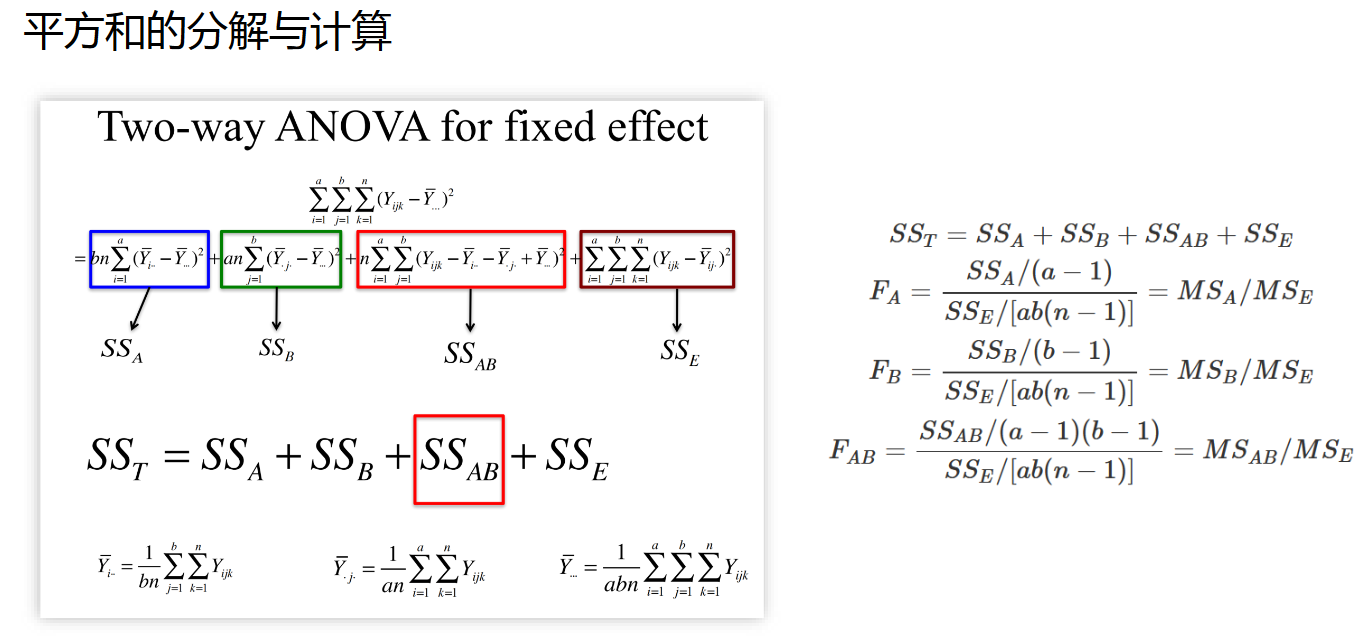

在R语言中,Two-way ANOVA的函数接口依然是 aov() ,需要注意如果要求带互作的ANOVA,则传入参数中两个因子之间的连接符需要使用星号 * ,如果不考虑互作,则使用 +
- 考虑因子A与因子B的互作:
aov(Y~A*B,data), 等价于aov(Y~A+B+A:B,data),其中A:B表示因子A与因子B的互作效应。 - 不考虑互作:
aov(Y~A+B,data)

交互作用的可视化
这一块并非上课重点,因此仅通过PPT列出相关函数接口以及使用效果,供参考。
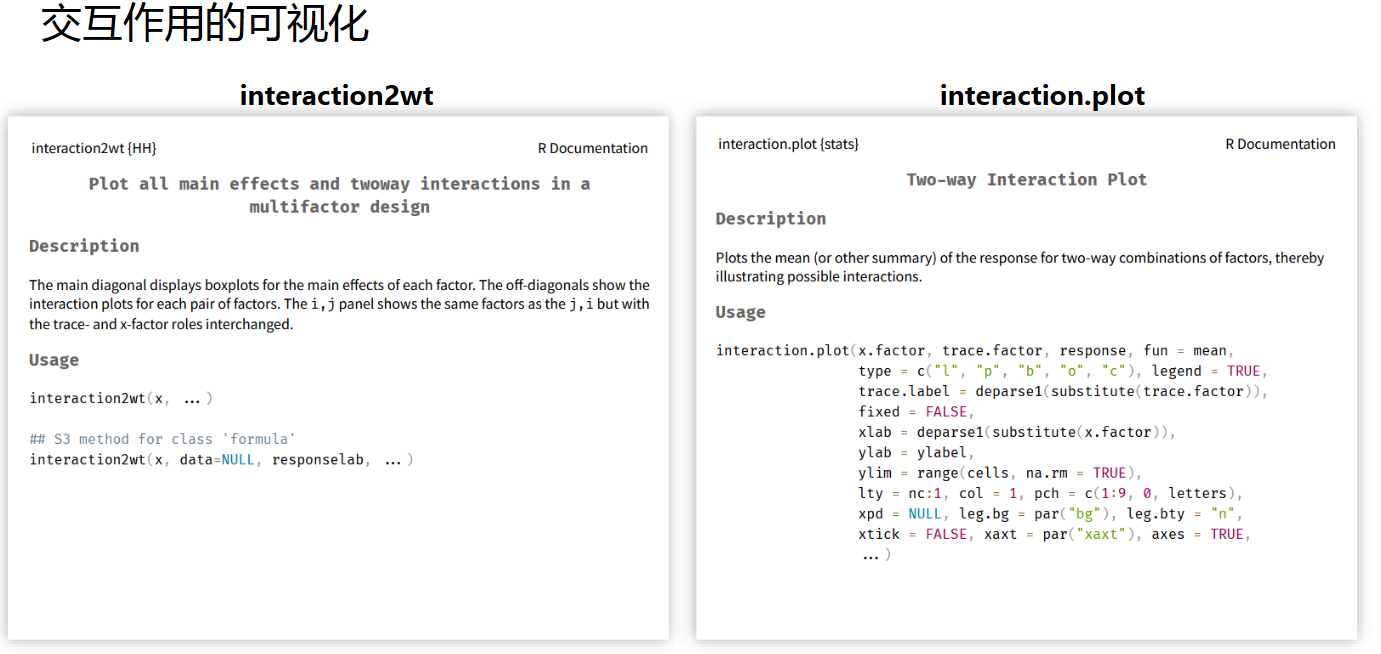
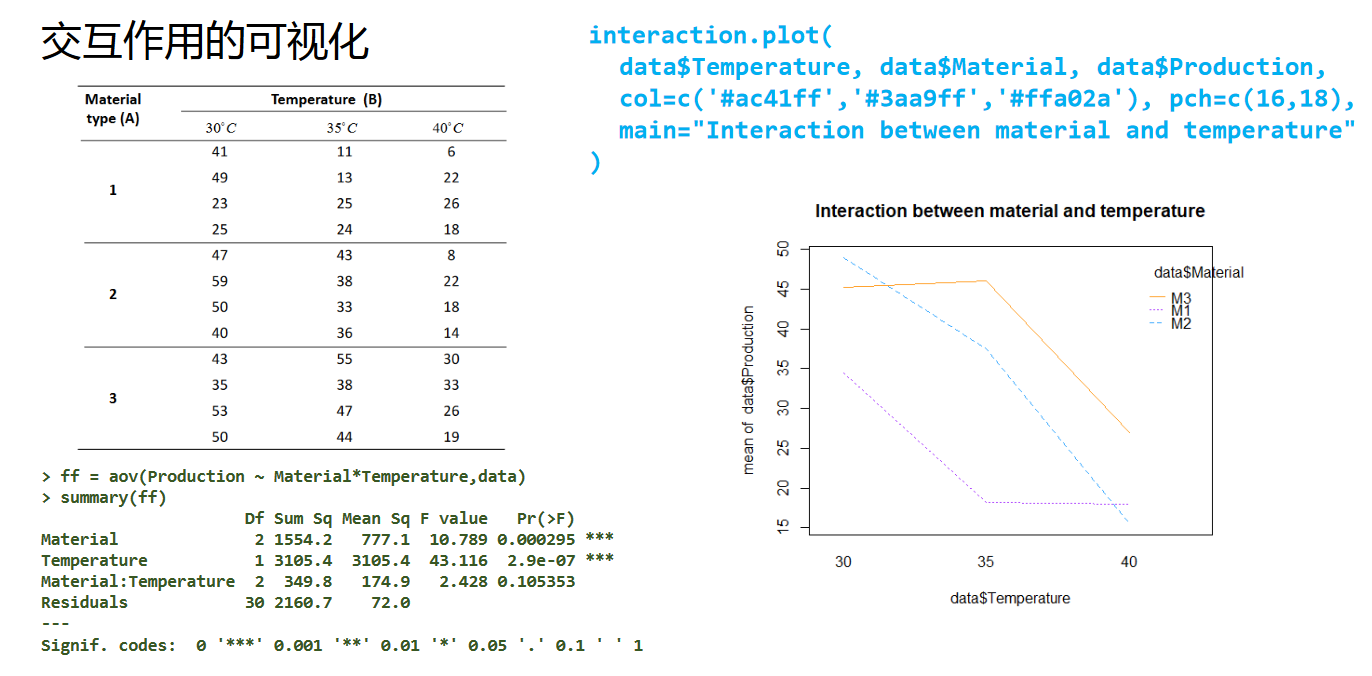
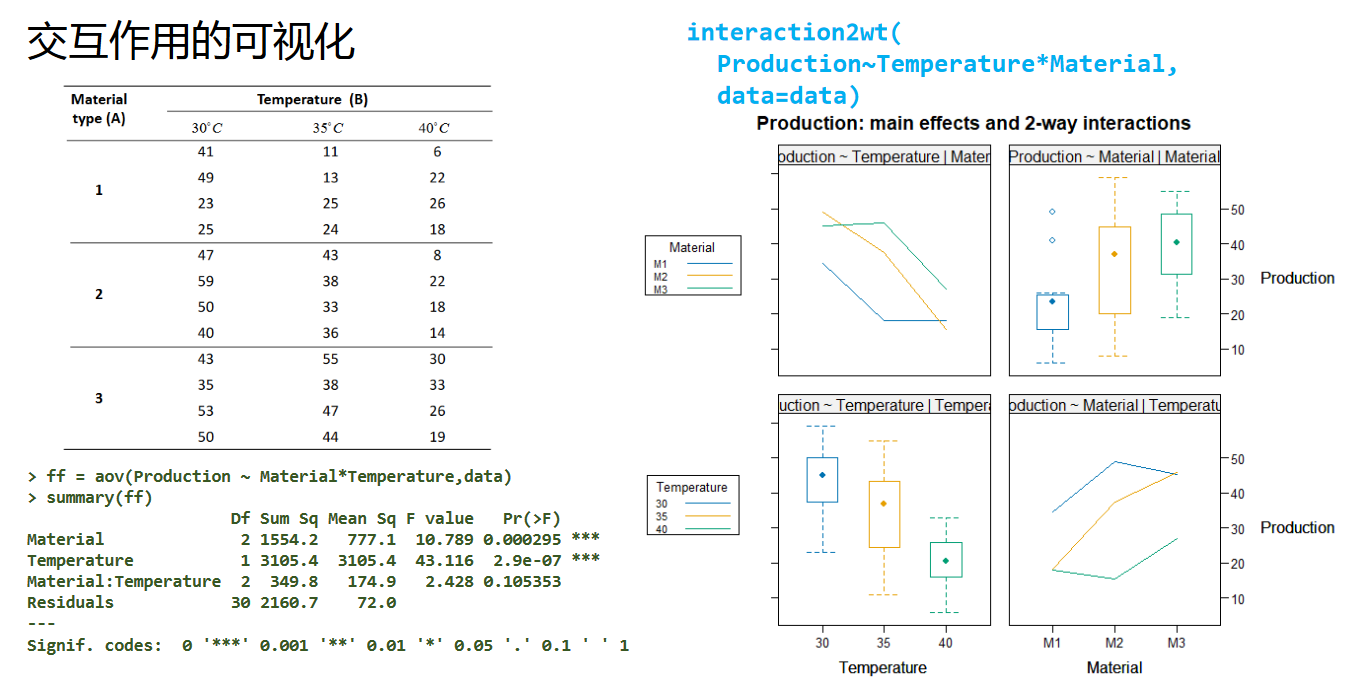
不带重复的双因素方差分析
如下图。Two-way ANOVA without replications不考虑互作,因此检验统计量只有两个, $F_{A}$ 和 $F_{B}$ ,分别检验因子A和因子B各自的效果,不检验二者的互作效果。

三、缺失值处理
这一块也不算课题重点,因此仅以一张PPT作为总结:
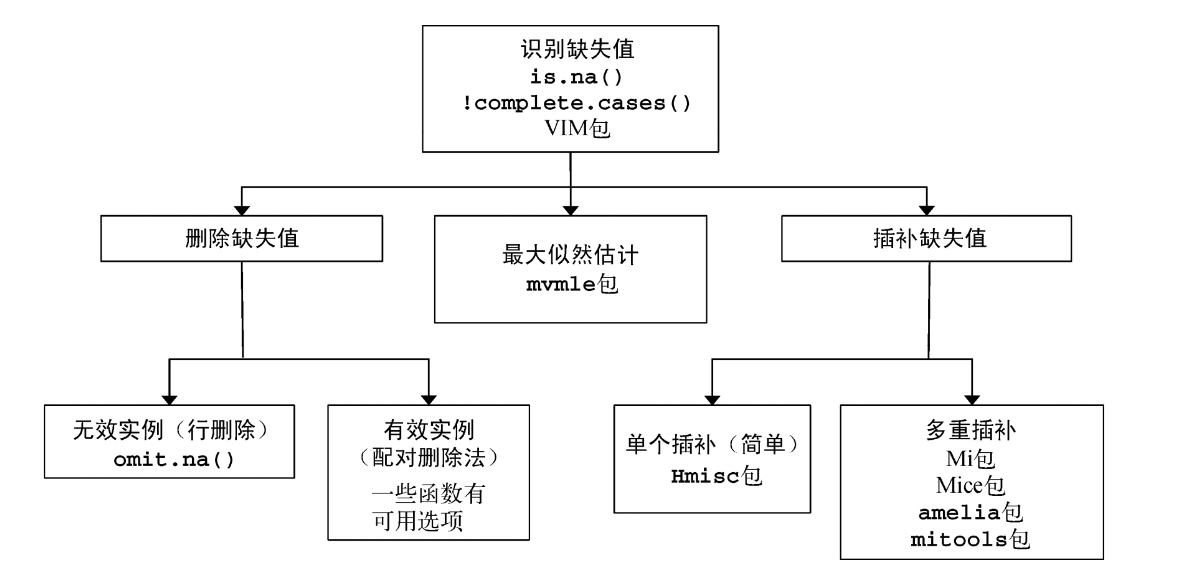
以上。