信息论学习笔记（一）

发表于 更新于 分类于

前段时间查文献的时候，偶然看到了一些算法里涉及到了信息论的相关知识。信息论我在几年前通过看书自学过，时间太久有些忘了，正好趁此机会重新复习一下。

参考书籍：机械工业《信息论基础（原书第二版）》（ELEMENTS OF INFORMATION THEORY SECOND EDITION），作者Thomas M. Cover, Joy A. Thomas

（不知道信息论的知识点有没有人感兴趣；如果有人看的话，我打算连续出几期关于信息论的笔记与知识点整理）

一、引言

信息论解答了通信理论中的两个基本问题：

  • 临界数据压缩的值（答案：熵H)
  • 临界通信传输速率的值（答案：信道容量C)。

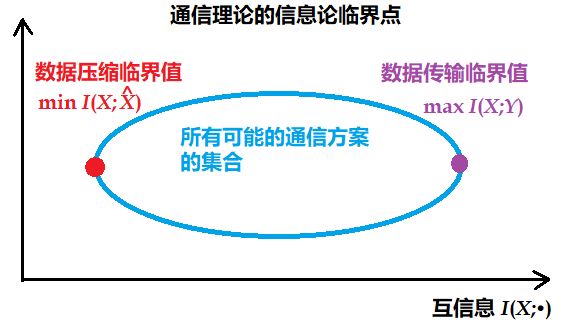
如果将所有可能的通信方案看成一个集合，那么今天的信息论描绘了这个集合的两个临界值，如下图所示（书中Fig1-2，此处重绘）。

  • 数据压缩达到最低程度的方案对应的是该集合的左临界值 $I(X;\hat X)$。所有数据压缩方案所需的描述速率不得低于该临界值。
    • 因为信源压缩的本质是用尽可能少的比特数表达随机变量 $X$ 。根据信息论的基本结论，最优压缩方案的码率必须等于 $H(X)$ ，即信源熵。
    • 如果压缩后的比特数少于这个值，则原信息将不可避免地丢失，因而 $H(X)$ 是数据压缩的下界。
  • 右临界值 $I(X;Y)$ 所对应方案的数据传输速率最大，临界值 $I(X;Y)$ 就是信道容量。
    • 在实际传输中，信道的容量 $C$ 是其可以无误传递信息的最大限值，即互信息 $I(X; Y)$ 最大可达到 $C$ 。如果发送的数据率超过 $C$ ，信道将无法完全可靠传输（会导致误码或未压缩的额外开销）。
  • 因此，所有调制方案和数据压缩方案都必须介于这两个临界值之间。

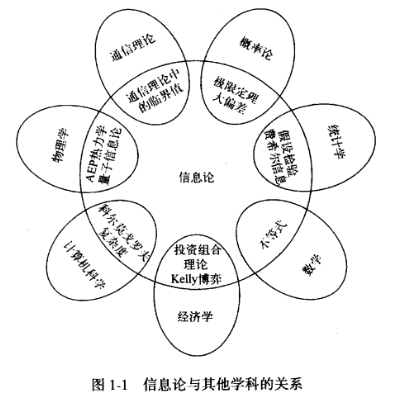
image.png

下图展示了信息论与其它学科的关系。

image.png

二、一些基本概念：信息熵、互信息、相对熵、通信信道

信息熵的定义：假设随机变量 $X$ 的概率密度函数为 $p(x)$ ，则 $X$ 的熵定义为：

$$
H(X) = -\sum_x p(x) \log_2 p(x) \tag{量纲：比特(bit)}
$$
$H(X)$ 的数学含义是描述该随机变量 $X$ 所需的比特数。

  • 例如，对于一个服从均匀分布的随机变量 $X$ ，如果 $X$ 有 32 种可能结果 ，那么用一个 5 比特长的字符串即可描述。（ $H(X) = -\sum_{1}^{32} (1/32) \log_2 (1/32) = \log_2 32 = 5$ ）

条件熵 $H(X|Y)$ ：在给定随机变量 $Y$ 的条件下，随机变量 $X$ 的熵。

互信息 $I(X;Y)$ : 由于 $Y$ 导致的 $X$ 随机变量不确定度的缩减量。其定义为：

$$
I(X;Y) = H(X) - H(X|Y) = \sum_{x,y} p(x, y) \log \frac{p(x, y)}{p(x)p(y)}
$$

  • 数学含义：互信息 $I(X; Y)$ 是 $X$ 与 $Y$ 之间信息相关程度的度量（也可以说，是 $X$ 与 $Y$ 之间信息独立程度的度量）。
    • $I(X; Y)$ 关于 $X$ 与 $Y$ 对称，取值范围为 $\geq 0$
    • $I(X; Y)>0$ ： $X$ 与 $Y$ 存在统计相关。
    • $I(X; Y)=0$ ： $X$ 与 $Y$ 相互独立。
  • 互信息 $I(X; Y)$ 是相对熵的特殊形式。

相对熵 $D(p||q)$ ：衡量两个概率密度函数 $p$ 与 $q$ 之间距离的指标（也就是上周文章中提到的KL散度）。 $D(p||q) \geq 0$ ，仅在 $p=q$ 时等于0 。

$$
D(p||q)=\sum_x p(x)log\frac{p(x)}{q(x)}
$$

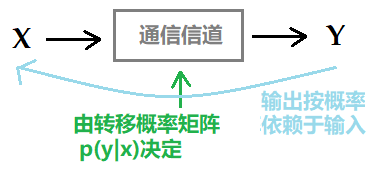
通信信道：通信信道是一个系统，系统的输出信号按概率依赖于输入信号。该系统特征由一个转移概率矩阵p(y|x)决定，该矩阵决定在给定输入情况下输出的条件概率分布。

  • 对于输入信号为X和输出信号为Y的通信信道，定义它的信道容量为 $C=max_{p(x)} I(X;Y)$

image.png