参数估计与统计推断相关知识点
本文为生统助教课备课过程的一些记录,主要涉及参数估计与统计推断(假设检验)的基本概念、参数检验与非参数检验的流程与相关概率分布模型(本文重点),以及R和python当中的相关函数接口。
一张图展示本文知识大纲:
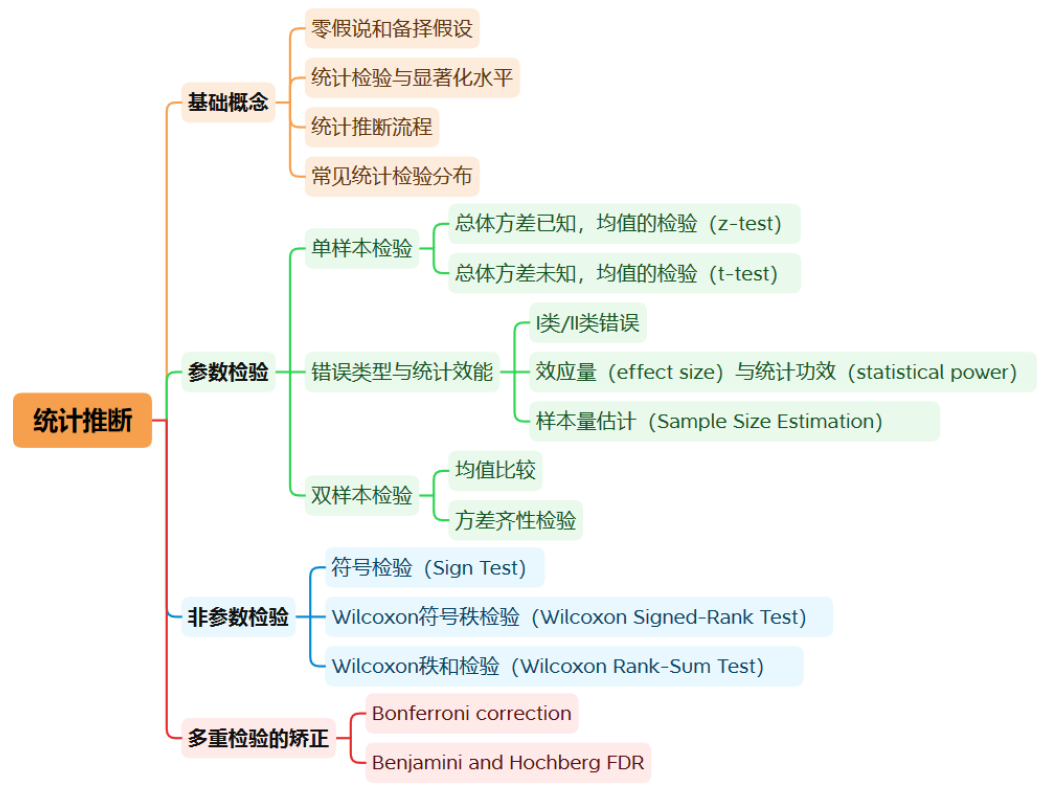
一、基础概念
(一)参数估计与统计推断的关系
参数估计:
- 从样本数据中推断出总体参数的值,并附带估计误差;
- 回答“什么是”或“什么样”的问题,例如某个投资的回报率是多少,某种药物的平均疗效是多少;
统计推断:
- 测试某个假设是否合理,评估样本数据与基于某个假设下的总体分布之间的差异;
- 回答“是”或“否”的问题,例如一种药物的效果是否比另一种更有效,一个批次中的产品是否达到了规定的标准;
估计通常需要基于一个假设来成立,例如正态分布假设。而前提假设的检验可以导致更准确的估计值,因为它使我们更清楚地理解参数的分布;
估计的结果也可以用作假设检验的基础,例如为了测试一个均值是否等于某个特定值,我们需要用样本均值来估计整个总体的均值。

(二)假设检验的基本流程
1.提出假设:
- H0: 原假设,基准或默认情况,假设总体参数没有变化或无差异
- Ha/H1: 备择假设
2.选择统计检验方法:
- 根据数据特征、问题类型及假设陈述等因素来选择适当的统计方法
- 如t检验、方差分析、卡方检验等;
3.选择显著性水平:
- 确定最小显著性水平(α),即拒绝零假设的概率阈值,通常设为0.05或0.01。
4.收集数据并计算检验统计量:
- 使用已选定的统计方法,并根据所测试的假设与收集的数据,计算出检验统计量的值,得到显著性水平。
5.判定结论:
- 当观察数据的结果与H0不一致时,有两种可能:
- 一是拒绝H0,接受Ha,即认为存在显著的差异或效应;
- 二是未能拒绝H0,即没有足够的证据表明Ha成立,无法判断是否存在显著的差异或效应。
- 需要根据检验统计量和显著性水平来做出判断,确定是上述可能中的哪一种
根据样本的不同,还可以将这一流程细化为单样本检验和双样本检验。

单样本检验如果需要使用参数检验(如z-test、t-test等),需要先检验数据是否服从正态分布。

双样本检验则需要更进一步,除了要检验数据是否服从正态分布以外,还需要进行方差齐性检验。
另外,这里还涉及到单侧和双侧检验的事情。单侧检验,一般回答的问题是“xx样本是否小于/大于yy样本或yy总体”;双侧检验,一般回答的问题是“xx样本的均值是否 不等于 yy样本或yy总体”。如何选择单侧或双侧检验,需要根据具体的问题类型来做决策。如果选择双侧检验,那么在查表寻找临界值时,需要使用一半的显著性水平(即α/2)去查表。
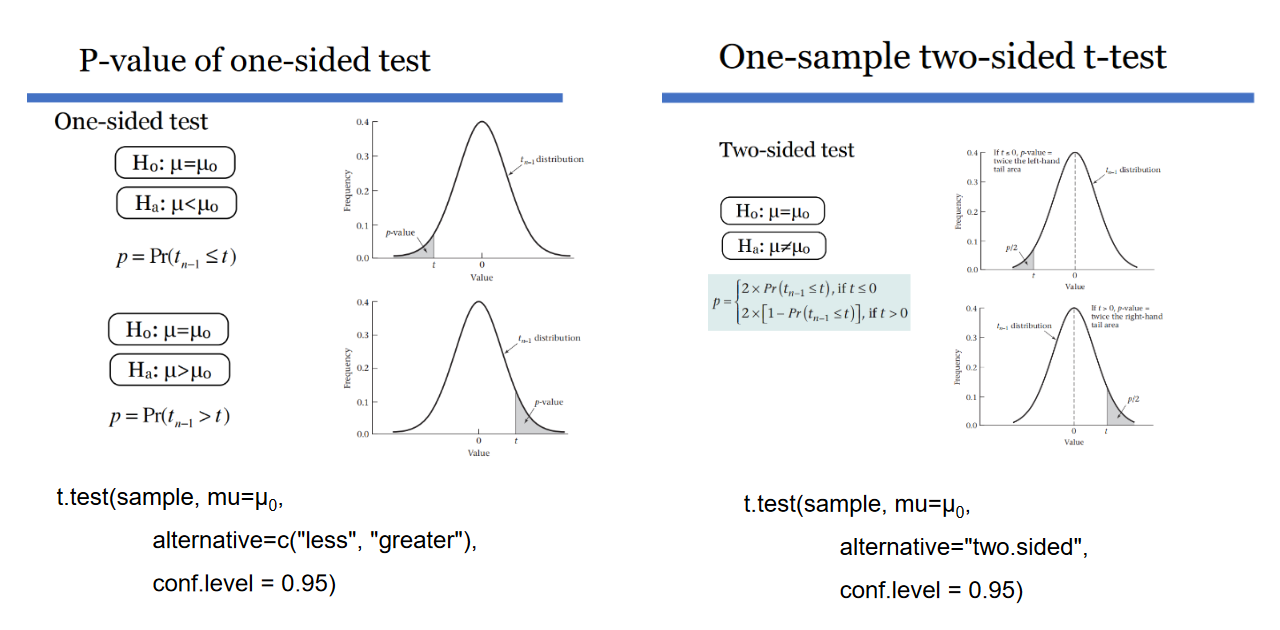
(三)假设检验所涉及到的一些统计分布模型
首先是正态分布。这是最常见的统计分布模型假设。

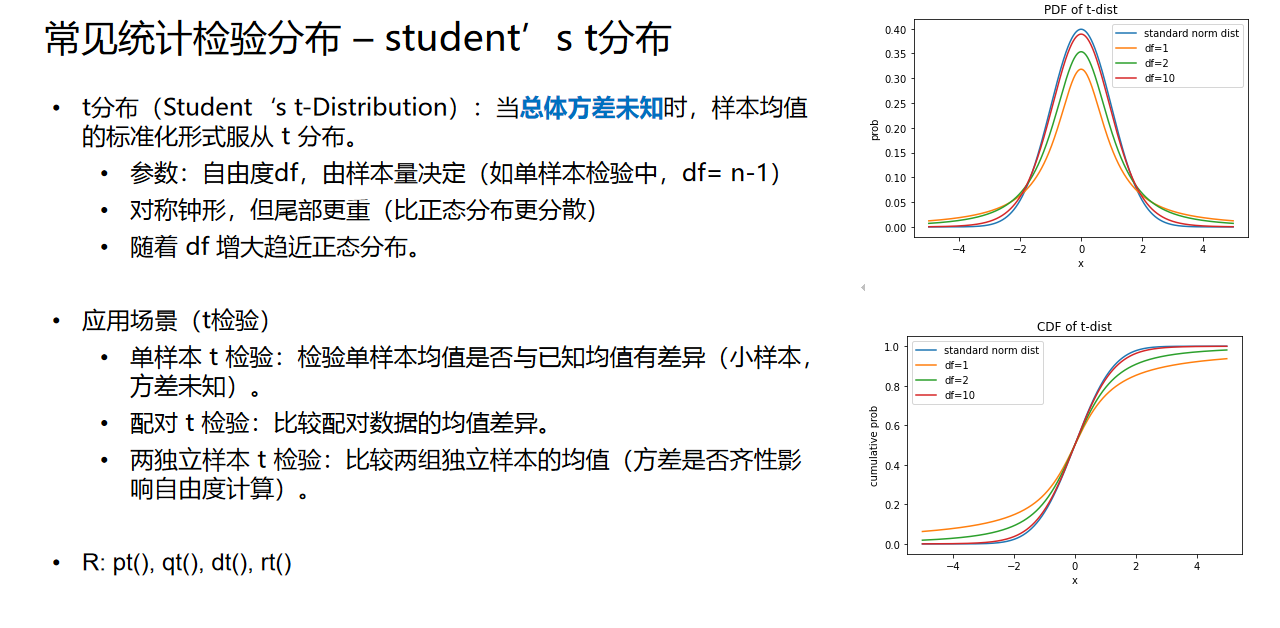
然后是student’s t分布。当总体方差未知时,样本均值的标准化形式服从这一分布,其形状与正态分布类似,但是尾部更重;参数df(“自由度”,等于n-1,其中n为样本量)越大,t分布越趋近于正态分布。
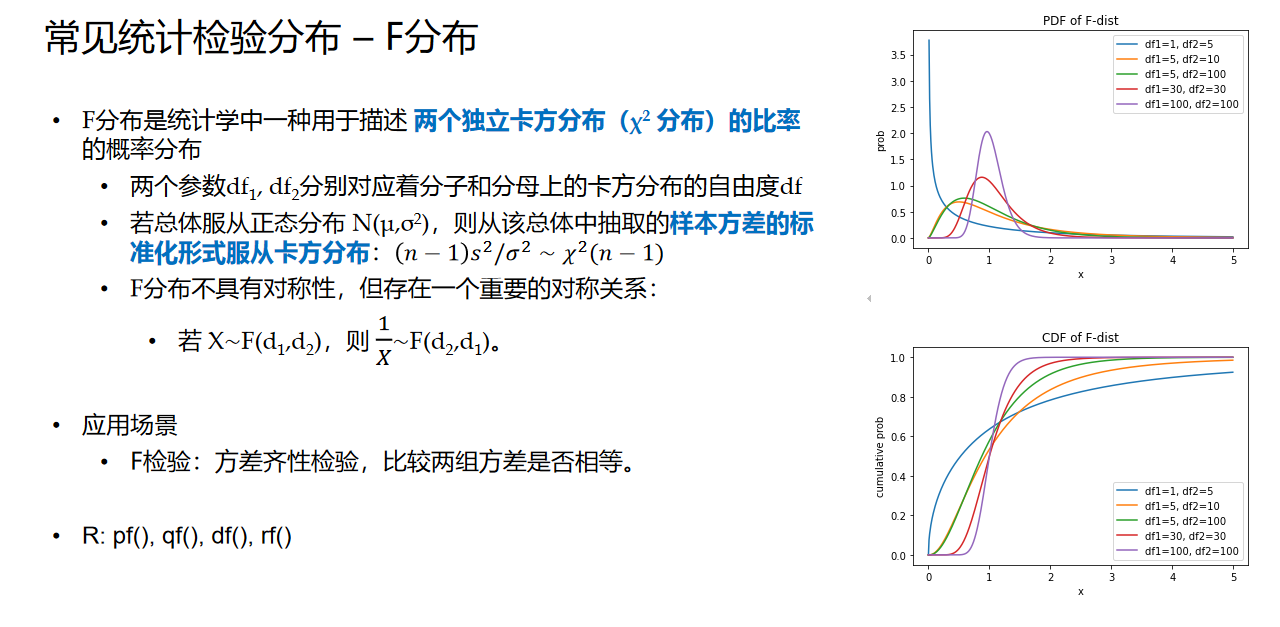
最后是F分布。其在方差齐性检验中有用。F分布描述的是两个独立卡方分布的比值,很巧的是正态总体的样本方差的标准化形式 $(n-1)s^2/σ^2$ 服从参数df等于n-1的卡方分布(n为样本量),因此可以用来检验方差是否齐次(检验的原理见下文)
二、参数检验
所谓参数检验,需要预设一个样本所服从的统计模型,如正态分布、t分布等。
(一)单样本检验
单样本检验,主要想回答的问题是:某个样本,是否来自于某个概率分布总体。
常用的两种检验方式是Z-test与T-test。
Z-Test 适用于以下情况:
- 总体标准差 $\sigma$ 已知。
- 样本量 $n$ 较大(通常 $n \geq 30$)。
T-Test 适用于以下情况:
- 总体标准差 $\sigma$ 未知,需要用样本标准差 $s$ 来估计。
- 样本量 $n$ 较小(通常 $n < 30$)。
| 检验类型 | 公式 |
|---|---|
| Z-Test | $Z = \frac{\bar{X} - \mu_0}{\sigma / \sqrt{n}}$ |
| T-Test | $T = \frac{\bar{X} - \mu_0}{s / \sqrt{n}}$ |
两者的主要区别在于分母部分:Z-Test 使用总体标准差 $\sigma$,而 T-Test 使用样本标准差 $s$。
Python当中的函数接口(单样本t-test):
1 | from scipy.stats import ttest_1samp |
R当中的函数接口:
1 | # Z-test,需要知道总体标准差sigma.x |
另外还有两个比较关键的概念:检验的效能(power),以及效应量(effect size)。相关知识点见下面的PPT页面截图。

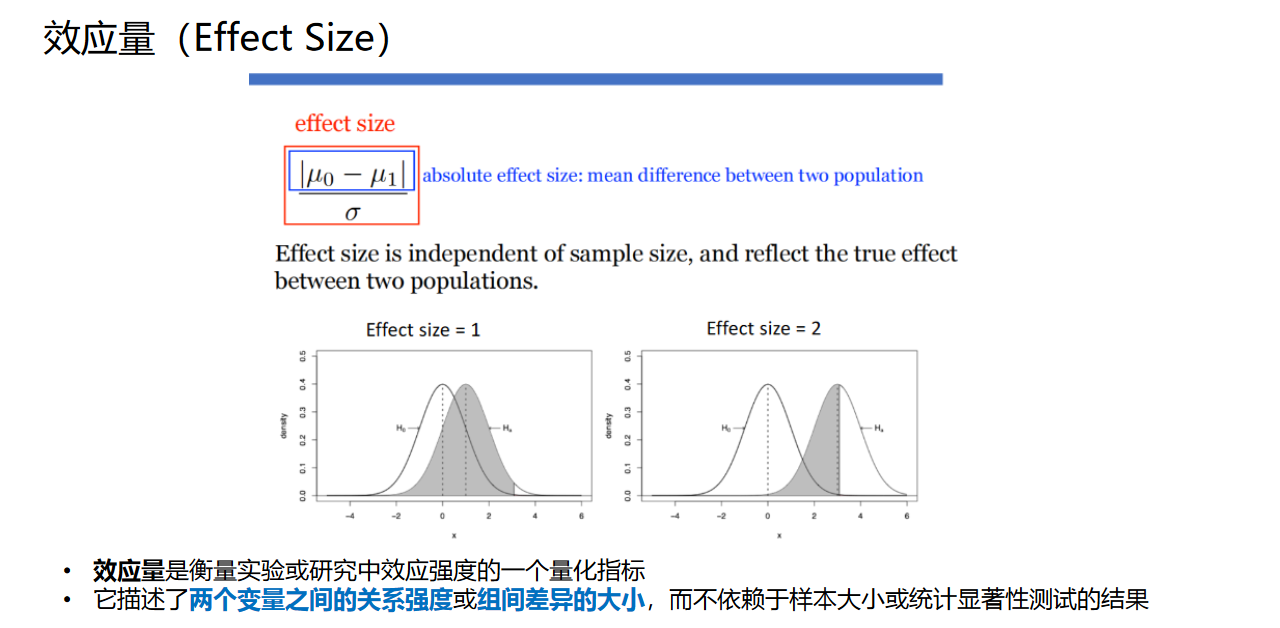


(二)配对样本t检验
某种意义上,配对样本t-test,可以看作一种特殊的单样本检验。因此,原理不在细讲。下面是python和R中调用配对样本t-test的方法:
Python:
1 | scipy.stats.ttest_rel(a, b, alternative='two-sided') |
R:(依然是t.test这个函数,但是需要指定参数paired = TRUE)
1 | t.test(x, y = NULL, alternative = "two.sided", mu = 0, paired = TRUE) |
(三)双样本独立t检验
双样本独立t检验,其检验统计量的计算方法如下(注意分母部分的处理):

如本文前面所述,双样本检验除了要检验数据是否服从正态分布以外,还需要进行方差齐性检验。下图为方差齐次检验的原理。
- F分布描述的是两个独立卡方分布的比值,很巧的是正态总体的样本方差的标准化形式 $(n-1)s^2/σ^2$ 服从参数df等于n-1的卡方分布(n为样本量)
- 我们把两个样本的样本方差的标准化形式相除,得到的统计量 $(s^2_1σ^2_2)/(s^2_2σ^2_1)$ 服从分布 $F(n-1,m-1)$ ,其中m,n分别是两个样本的样本量
- 如果这两个样本来自相同方差的总体,那么 $σ_1=σ_2$ ,在分式中这两项可以约分,最终得到的形式 $s^2_1/s^2_2$ 依然服从分布 $F(n-1,m-1)$
- 因此,我们只需要检验 $s^2_1/s^2_2$ 是否服从分布 $F(n-1,m-1)$ ,即可得知两个样本各自的总体方差是否相等。

三、非参数检验
如题。非参数检验不依赖总体的分布,因此也有很广泛的应用。
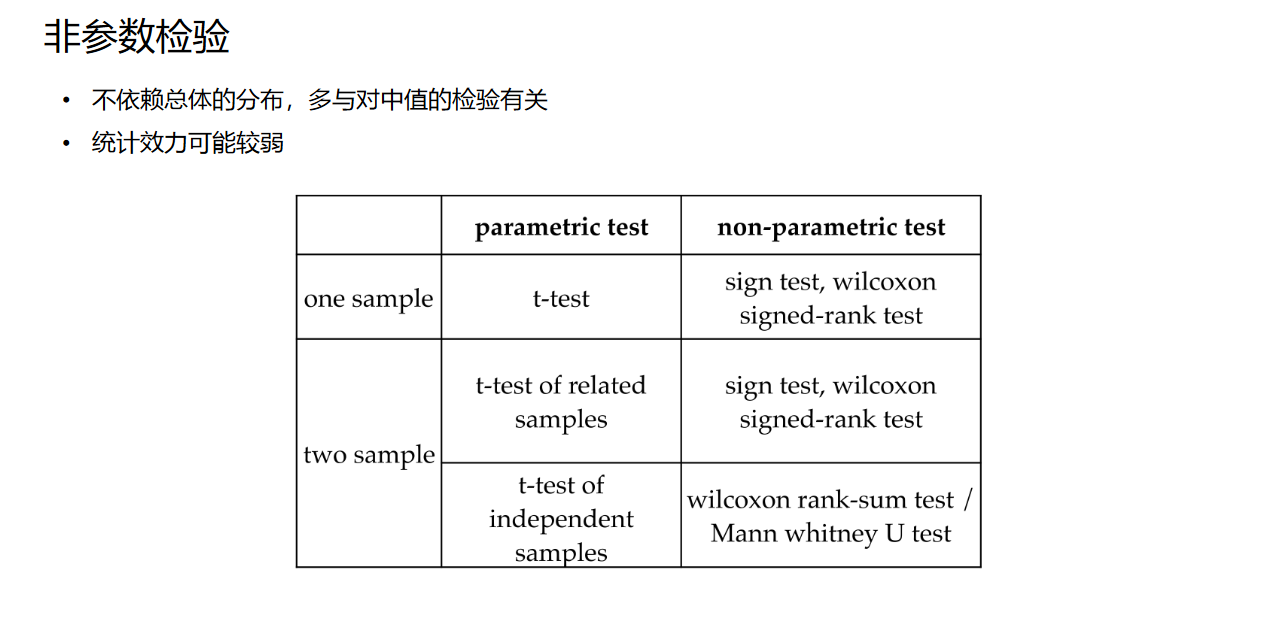
1、符号检验:只需要统计样本中超过某一标准值M0的样本的数量,基于二项分布的概率模型进行检验。

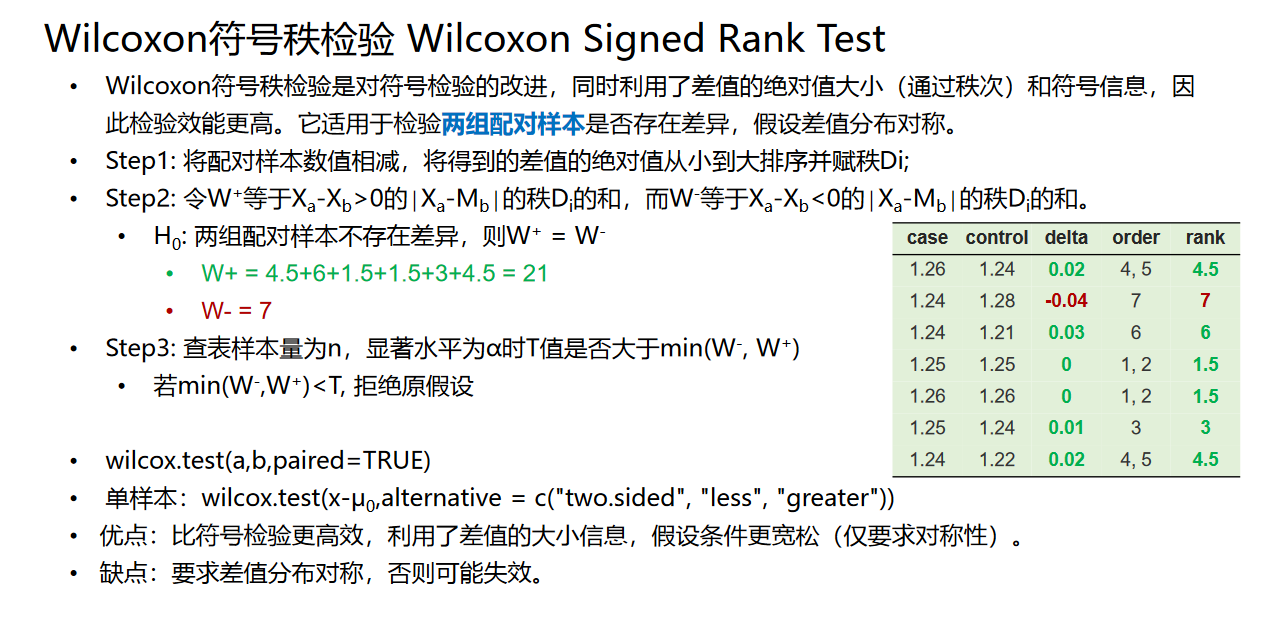
2、Wilcox符号秩检验:在符号检验的基础上考虑秩次信息。适合配对样本检验
3、Wilcox秩和检验:两组样本混合在一起,然后编秩次(即,从大到小对样本编号),随后计算样本量较小的一组的秩次之和,查表进行检验。

四、多重矫正
当假设检验的过程重复多次时,总体错误概率(“家族错误率”,Family-wise error rate,FEWR)会不断增长。多重矫正就是要解决这个问题。

常用的方法包括bonferroni矫正、Holm方法、BH矫正等。
