概率分布模型相关知识点整理

本文为生统助教课备课过程的一些记录，主要涉及概率分布模型的定义、几种离散概率模型之间的关系，以及R和python当中这些概率模型的接口。

一、一些先导概念

随机变量：

描述随机事件的数值特征，是一个定义在样本空间上的实值函数，它将每个样本点映射到一个实数

根据变量的取值可以分为：

• 离散型随机变量(Discrete random variable)：取值为可数的实数，通常与可以计算或列举的事件有关，比如患者在一定时间内发生的癫痫发作次数/接受治疗的次数；患者的致病突变携带数（0/1/2）。代表的数学分布有：二项分布，泊松分布，负二项分布，超几何分布
• 连续型随机变量(Continuous random variable)：取值为给定范围区间内的任意实数，通常与涉及测量或数量的事件相关，比如患者的身高、体重、血液药物浓度、某基因表达量。代表的数学分布有：正态分布，gamma分布

概率分布与累积分布函数：

描述随机变量取值概率的函数。

• 概率分布函数 ：描述随机变量取值概率的函数
  • 概率质量函数(probability mass function,PMF) → 离散型随机变量
  • 概率密度函数(Probability Density Function,PDF) → 连续型随机变量
  • $P(X = x) = p(x), P(a ≤ x ≤ b)=P(X ≤ b)–P(X < a-1)$
• 累积分布函数 ：描述随机变量小于或等于某个特定值的概率的函数
  • cumulative distribution function, CDF
  • 连续型随机变量的CDF是连续函数，离散型的CDF是阶梯函数
  • $F(x)=P(X\leq x)$
  • $P(a\leq x\leq b)=\int_a^bf(x)dx$
• 概率分布函数的特征：
  • $\sum P(X)=1$
  • $0\leq P(X) \leq 1$
• 概率分布函数的统计量：
  • 均值/期望： $E(x)=\mu=\sum xP(x)$
  • 方差：$Var=\sigma^2=E[(x-\mu)^2]=\sum[(x-\mu)^2P(x)]=\sum x^2P(x)-\mu^2$

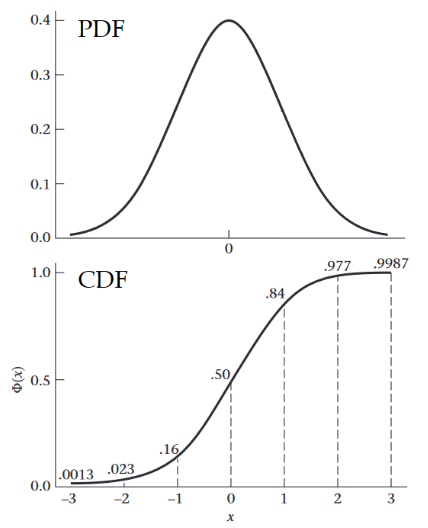
如下图是标准正态分布的概率密度函数（PDF）和累积分布函数（CDF）。可以看出，CDF相当于是对PDF的积分。（Adapted from: Bernard Rosner.Fundamentals of Biostatistics(8th).p118-125）

二、几种概率分布模型

（一）离散概率分布

1. 二项分布

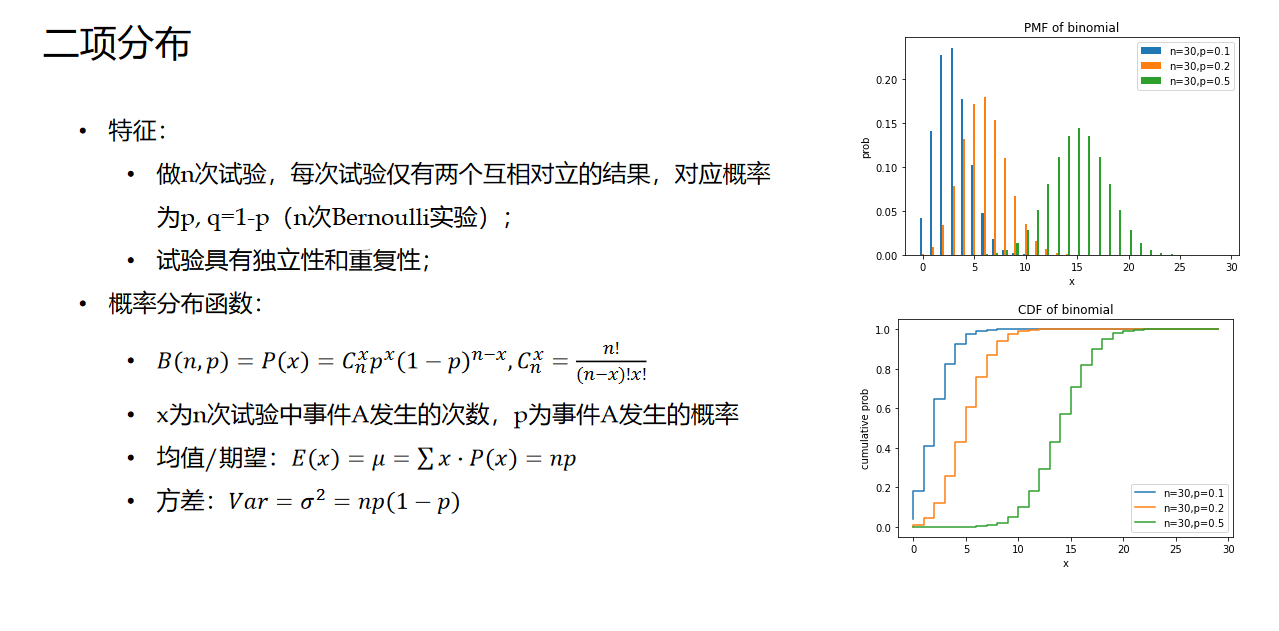
2. 负二项分布

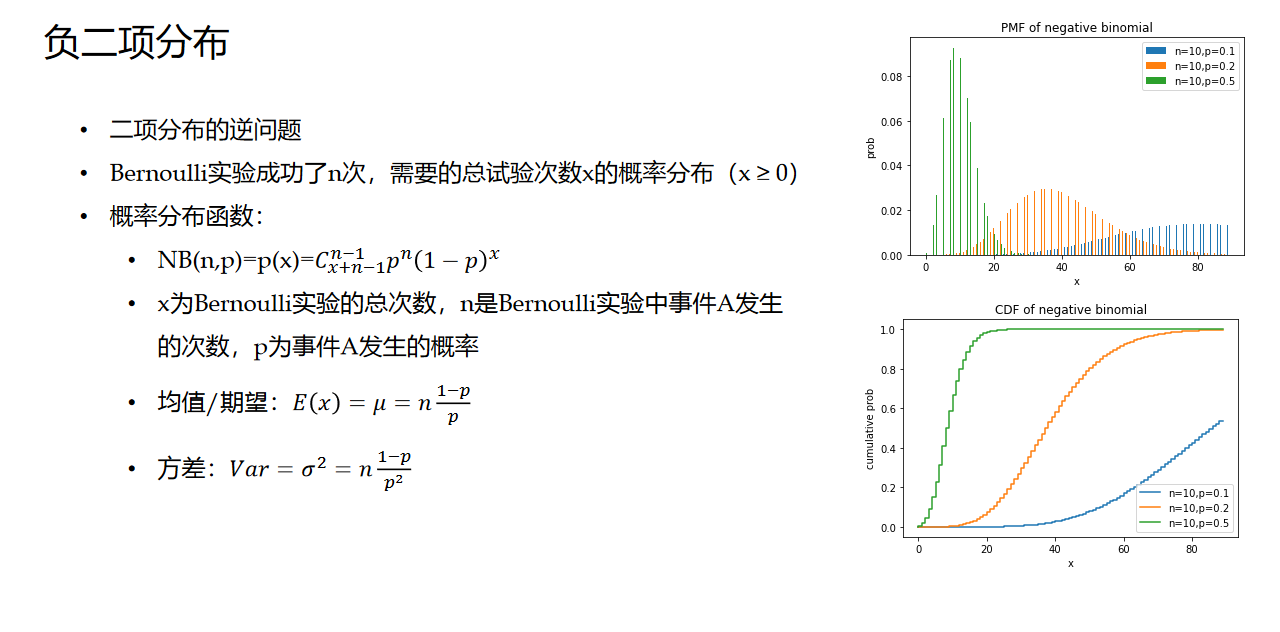
3. 超几何分布

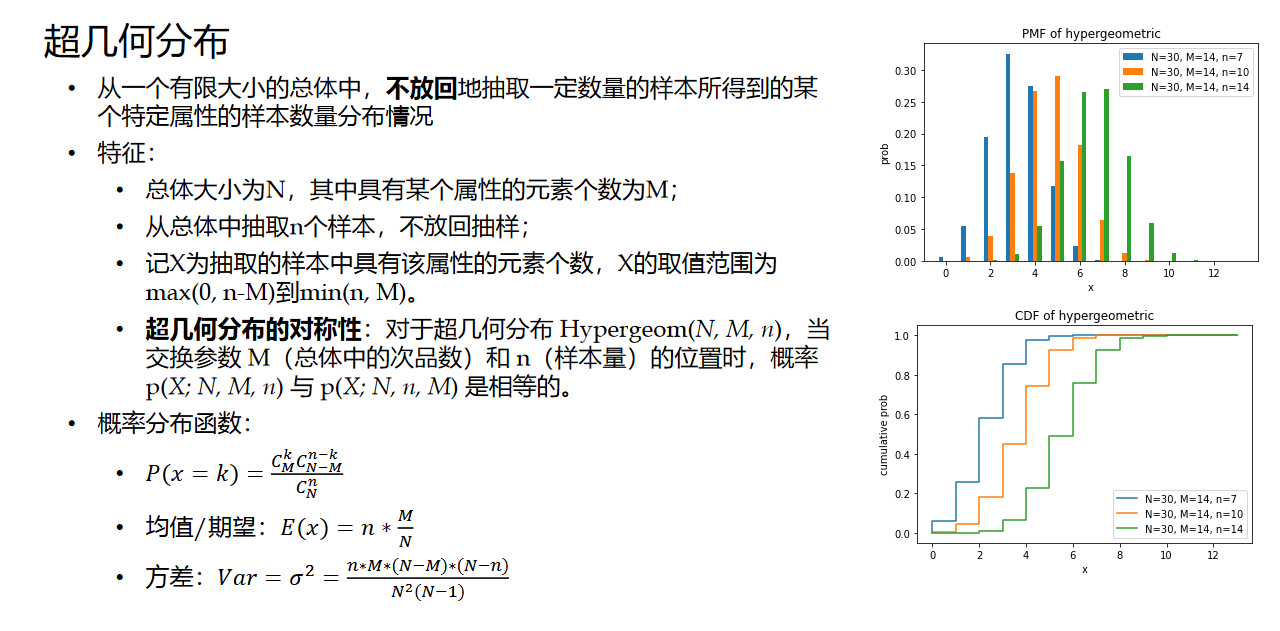
4. 泊松分布

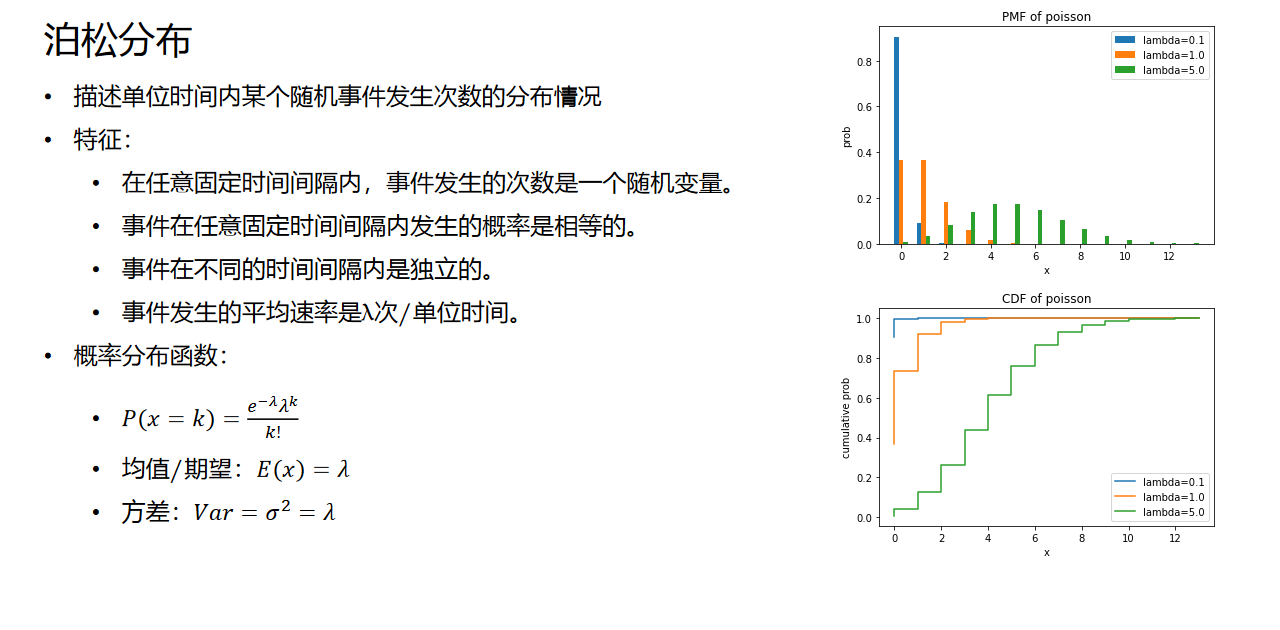
（二）连续概率分布

1. 正态分布

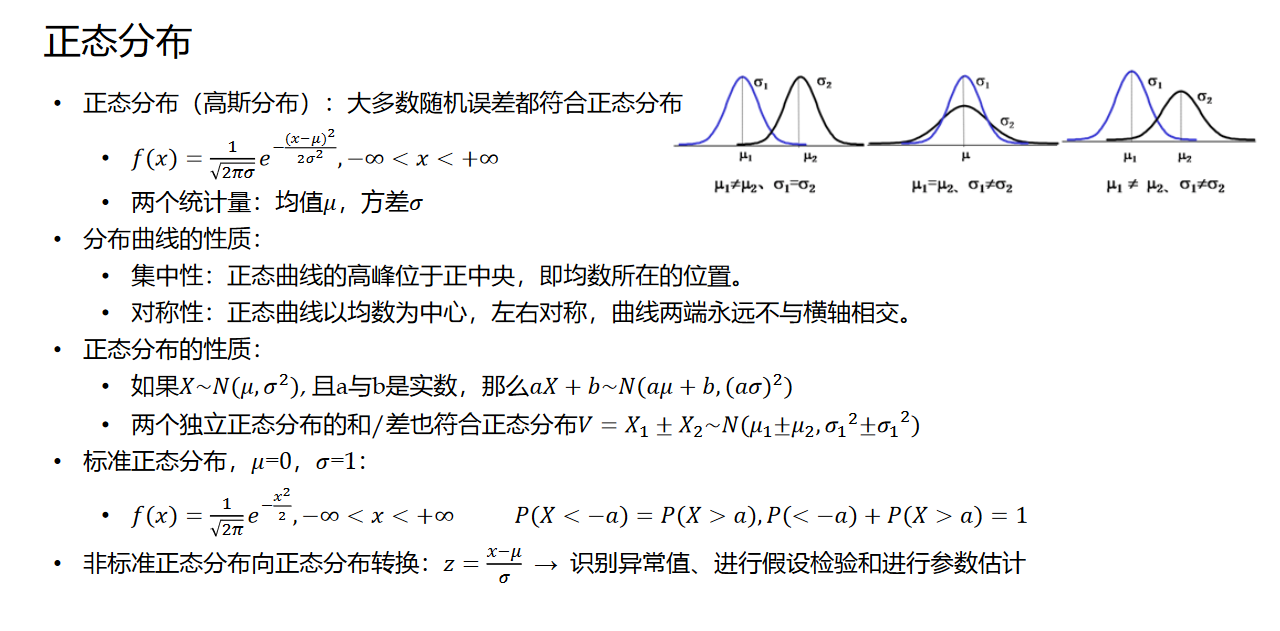
说到正态分布，就得提一下中心极限定理——这是两个紧密相关的概念。

中心极限定理

• 如果从总体中随机地抽取大量的样本，并且这些样本之间相互独立，并且总体的分布没有过多的偏态和峰度等特殊的性质，那么这些样本的均值的分布会近似为一个正态分布。
  • 更具体地说，随着样本大小的增加，这个近似程度会越来越高；
• 估计总体均值时，如果总体分布未知，可以利用中心极限定理来使用样本均值的正态近似分布来估计总体均值的置信区间；
  • 具体来说，若群体均值为均值为μ，标准差为σ，则样本均值为μ，标准差为σ/√n，n为抽样样本量
• 中心极限定理并不适用于所有类型的分布。例如，如果总体分布是长尾分布（如幂律分布），那么中心极限定理可能不适用，因为长尾分布的特殊性质会导致样本和的分布无法近似为正态分布。

例如，假设在某地一个足够大的学生群体当中，测得这些学生的身高的总体均值为170cm，总体标准差为5cm。如果我们从这个大群体里面抽取9个人的样本，那么这样的抽样样本服从什么样的分布？抽样样本均值大于171cm的概率是多少？

使用中心极限定理，我们可以求得这个sample size为9的样本服从均值为170cm、标准差为 $5\text{cm}/\sqrt{9}=5/3\text{cm}$ 的正态分布。在此基础上，我们可以求出抽样样本均值大于171cm的概率：

$$
P(\bar{x}\geq 171|x \sim N(170,(5/3)^2))=P(Z\geq 0.6|Z \sim N(0,1))=27.423%
$$

（更具体的过程，以及相应的R代码如下图所示）。

指数分布

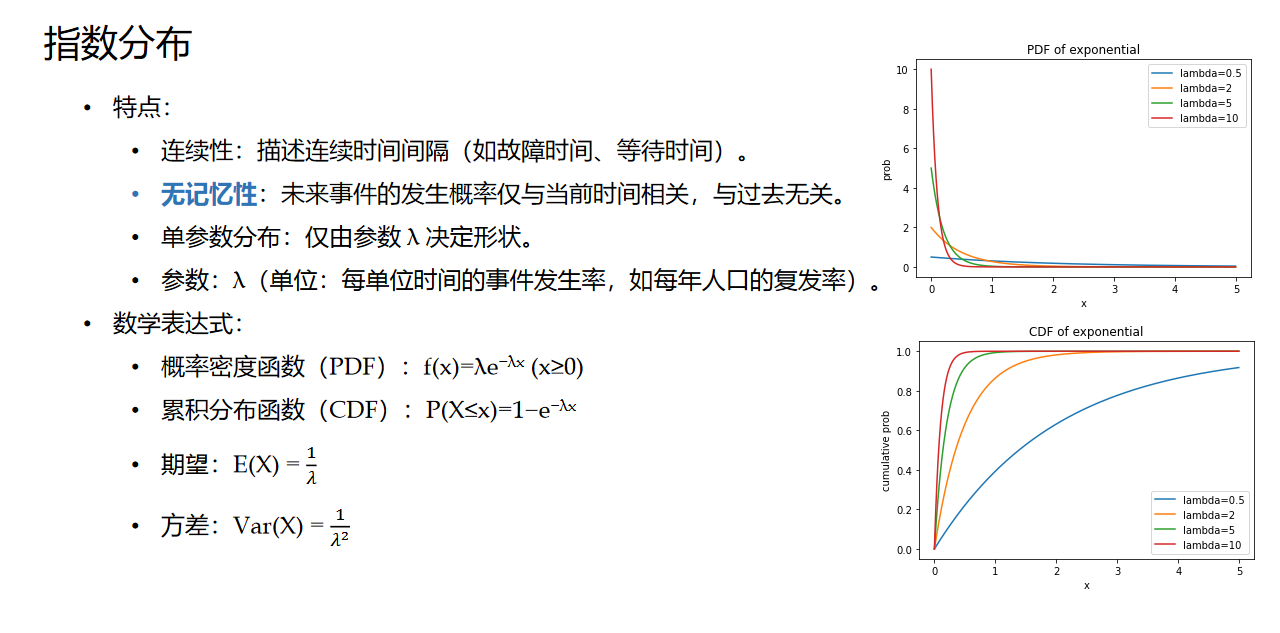
指数分布有一个很重要的特性是无记忆性。一个例子如下：

在一项生物医学研究中，某种疾病的患者在接受治疗后首次复发的时间服从指数分布（以年为单位），平均复发时间为5年。假设患者在2年内没有复发，计算未来3年内复发的概率。

首先我们计算参数：均值μ=5，因此指数分布的参数λ=1/5=0.2。随后我们利用指数分布的无记忆性，患者未来3年内复发的概率与前两年的情况无关，因此有

$$
P(x\leq 2+3|x>2)=P(x\leq 3)=1-e^{-3λ}\approx 0.4512=45.12%
$$

三、不同概率分布模型之间的关系

（一）几种离散概率分布模型之间的关系

如下图所示：

简单来说，二项分布、超几何分布、泊松分布都是在描述抽样实验的概率，但各有不同：

• 二项分布和泊松分布都是放回抽样，超几何分布是无放回抽样（当总体大小N足够大时，无放回抽样对总体的影响足够小，此时可以用二项分布去近似替代超几何分布）
• 二项分布的抽样次数有限，但是泊松分布的抽样次数无限（当实验次数n足够大时，可以用泊松分布去近似替代二项分布）

另外，下面是一个公式推导，用来说明二项分布与泊松分布的关系：

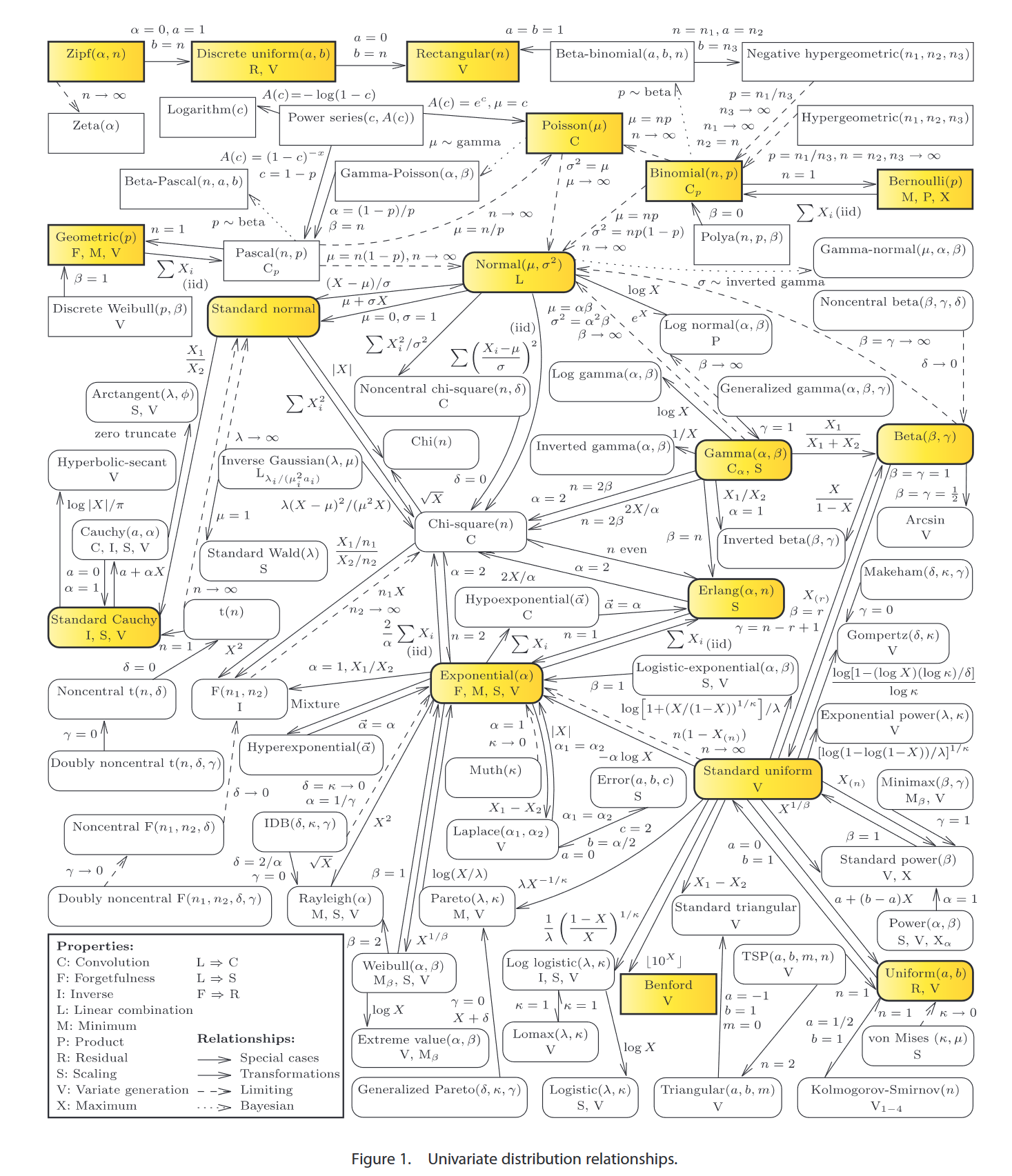
（二）各个概率分布模型之间的关系

如下图所示。具体解释略。

这张图片也可以在下面这两个网站上访问：

• William & Mary Univeristy - Univariate Distribution Relationships
• University of Cambridge - Univariate Distribution Relationships

四、概率分布模型与生物学研究

（一）三种离散概率分布的应用

二项分布：

• 母体基因型为Aa的自交或异交子代中，表现为aa基因型的个体数量
• 两种不同药物治疗一个病人时，其中一种药物获得治愈的数量

超几何分布：

• 从一个含有不同基因型的总体中随机抽取n个个体，其中含有特定基因型的个体数量
• 在一个人群中，检测到特定疾病的个体数量

泊松分布：

• 细胞分裂时，某个基因突变发生的次数
• 一个时间单位内，某种疾病的发病次数

（二）基因表达差异分析（显著性检验）与概率分布模型

在这一类情形中，我们主要关注的问题是，基因在不同样本间的表达水平应该符合什么分布？

• RNA-Seq得到的read counts，一个样本有多少条该基因的转录本 → 离散型随机变量；
• 泊松分布：描述独立事件在固定时间或空间内发生的次数。其统计学特征为 μ=σ。
• 虽然泊松分布是一种很好的模型，但在生物学实验中，多个重复测量通常会存在一些共性或相关性，例如由于技术误差、样本处理过程中的系统误差等原因（ 泊松分布可能不适用 ）。
• 负二项分布是一种更为合适的计数数据模型，它可以很好地描述多个重复测量数据之间的相关性和异质性。在负二项分布中，每个计数数据的方差可以比其均值大得多，因此负二项分布可以很好地描述实验数据中的过度离散现象；
  • 在DESeq2的分析中，负二项分布被转化为对数空间中的正态分布来进行统计分析

五、在R语言和Python语言中计算概率分布

（一）R语言

关于R语言的安装方法，可以参考下图：

R语言的默认环境中已经预先加载了一系列概率分布模型的包和函数。这些函数有独特的命名规律，如下所述：

前缀命名	含义	解释
d	密度函数	PMF或PDF
p	分布函数	CDF
q	分位数函数	CDF的反函数
r	随机数生成函数	生成一组服从特定分布的随机数

后缀命名	概率分布模型
norm	正态分布
exp	指数分布
t	t-分布
f	f-分布
binom	二项分布
nbinom	负二项分布
pois	泊松分布
hyper	超几何分布
……	……

例如：泊松分布的相关函数如下：

• 概率质量函数： dpois(x, lambda)
  • x: 事件发生次数
  • lambda: 单位时间/空间内的平均事件数
• 分布函数：ppois(q, lambda)
  • q: 分位点
• 分位数函数：qpois(p, lambda)
  • p: 概率值
• 随机数生成：rpois(n, lambda)
  • n: 生成的随机数个数

其他概率分布模型以此类推。

（二）Python（Scipy包）

Python标准库中提供了一些概率分布模型的代码支持，但不多。因此更多的时候，我们会使用scipy。

如果电脑上没有安装Python，可以使用下面的方法进行安装：

# 两个安装指令任选其一
python -m pip install scipy
conda install scipy

Scipy中，涉及概率分布的接口在 scipy.stats 模块下，相关内容可以参考 官方文档 。

下表列出了一些常用的离散分布模型的接口：

离散分布模型	函数接口	文档链接
二项分布	scipy.stats.binom	https://docs.scipy.org/doc/scipy/tutorial/stats/discrete_binom.html
负二项分布	scipy.stats.nbinom	https://docs.scipy.org/doc/scipy/tutorial/stats/discrete_nbinom.html
超几何分布	scipy.stats.hypergeom	https://docs.scipy.org/doc/scipy/tutorial/stats/discrete_hypergeom.html
泊松分布	scipy.stats.poisson	https://docs.scipy.org/doc/scipy/tutorial/stats/discrete_poisson.html
……	……	……

Scipy中的离散分布模型，其相关函数如下：

• 概率密度函数 pmf
• 累积分布函数 cdf
• 分位数函数 ppf
• 随机数生成 rvs

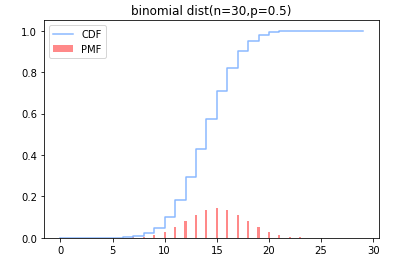
下面是一个二项分布的示例。注意，由于二项分布是一种离散概率分布模型，此处使用柱状图和阶梯图表示了PMF和CDF的曲线。

## 二项分布
# https://docs.scipy.org/doc/scipy/tutorial/stats/discrete_binom.html
from scipy.stats import *
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0,30)
dist = binom.pmf(x,n=30,p=0.5) # 获取概率密度
cdf  = binom.cdf(x,n=30,p=0.5) # 获取累积概率分布
plt.bar(x,dist,label="PMF",color="#ff8989",width=0.2)
plt.step(x,cdf,label="CDF",color="#89b8ff")
plt.legend()
plt.title("binomial dist(n=30,p=0.5)")
plt.show()

下表列出了一些常用的连续分布模型的接口：

连续分布模型	函数接口	文档链接
正态分布	scipy.stats.norm	https://docs.scipy.org/doc/scipy/tutorial/stats/continuous_norm.html
指数分布	scipy.stats.expon	https://docs.scipy.org/doc/scipy/tutorial/stats/continuous_expon.html
卡方分布	scipy.stats.chi2	https://docs.scipy.org/doc/scipy/tutorial/stats/continuous_chi2.html
t-分布	scipy.stats.t	https://docs.scipy.org/doc/scipy/tutorial/stats/continuous_t.html
F-分布	scipy.stats.f	https://docs.scipy.org/doc/scipy/tutorial/stats/continuous_f.html
……	……	……

Scipy中的连续分布模型，其相关函数如下：

• 概率密度函数 pdf（注意和离散分布的函数接口不一样）
• 累积分布函数 cdf
• 分位数函数 ppf
• 随机数生成 rvs

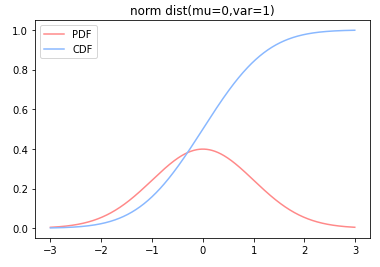
下面是一个正态分布的示例。注意，由于正态分布是一种连续概率分布模型，此处使用折线图（连续曲线）表示了PMF和CDF的曲线。

## 正态分布
# https://docs.scipy.org/doc/scipy/tutorial/stats/continuous_norm.html
from scipy.stats import *
import numpy as np
x = np.arange(-3,3,0.01)
dist = norm.pdf(x,loc=0,scale=1) # 获取概率密度
cdf  = norm.cdf(x,loc=0,scale=1) # 获取累积概率分布
plt.plot(x,dist,label="PDF",color="#ff8989")
plt.plot(x,cdf,label="CDF",color="#89b8ff")
plt.legend()
plt.title("norm dist(mu=0,var=1)")
plt.show()

调用函数时的一些注意事项

• Scipy包中的所有概率分布函数都有两个参数，loc和scale，即位置参数和形状参数。
  • 在一些分布当中，这两个参数有各自的数学含义（如正态分布中loc为均值，scale为标准差；指数分布中scale代表1/λ）；
  • 另一些分布当中，则需要用到其他参数（例如二项分布有额外的参数n和p）
• 一些分布模型，在不同文献和软件（包括scipy和R）中可能采用不同的参数化方式，导致传参时需要注意
• 调用函数时的实操建议
  • 文档查阅要点
  • 明确分布的定义
  • 核对参数名称与数学符号的对应关系
  • 通过简单案例验证参数传递的正确性