生命表、矩阵群体模型与生存曲线

发表于 分类于

在生态学和临床医学中，有这样几个非常类似的概念很容易混淆：生命表（生态学），存活曲线（生态学），生存分析与生存曲线（临床医学）。这篇文章中我们将辨析一下这些概念，并介绍生态学研究中的矩阵群体模型（Matrix Population Models，MPM），后者是与生命表密切相关的一个数学模型。

生命表（life table）（生态学）：

死亡是决定种群数量动态变化的关键因素之一。我们可以用生命表(life table)这种有用的工具来描述种群的死亡过程。有关死亡率的信息是通过调查不同生活时期死亡个体的数目而获得的，这些数据通过生命表来呈现和分析。动态生命表总结的是一组大约同时出生的个体从出生到死亡的命运，这样的一组个体称作同生群(cohort),这样的研究叫做同生群分析(cohort analysis)。还有一类生命表是根据某一特定时间对种群做一年龄结构的调查资料而编制的，称作静态生命表。静态生命表一般用于难以获得动态生命表数据的情况下的补充。——《基础生态学》pp.71-74

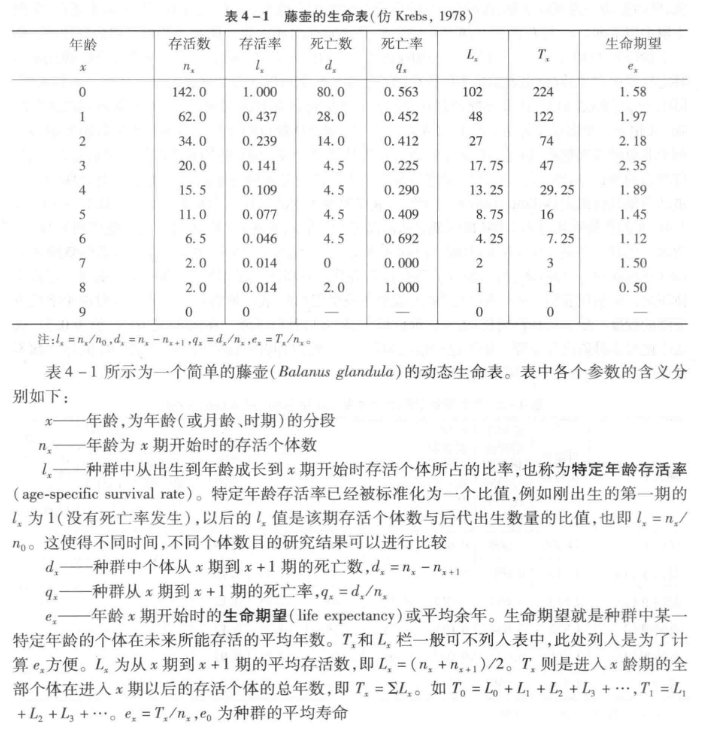
image.png

表中 $l_x$ 这一栏是最重要的，描述了种群在各年龄段的存活率。另一重要的栏目是 $q_x$ 栏，描述了种群死亡率随年龄而变化的过程。 $e_x$ 栏主要用于人类生命表，对保险业制定不同年龄人群的保险政策有实用价值。

存活曲线（survivorship curve）（生态学）

存活率数据通常可用图表示为存活曲线(survivorship curve)。以lg(nx)栏（或lg(lx)栏）对x栏作图即可得存活曲线（图4-7）。

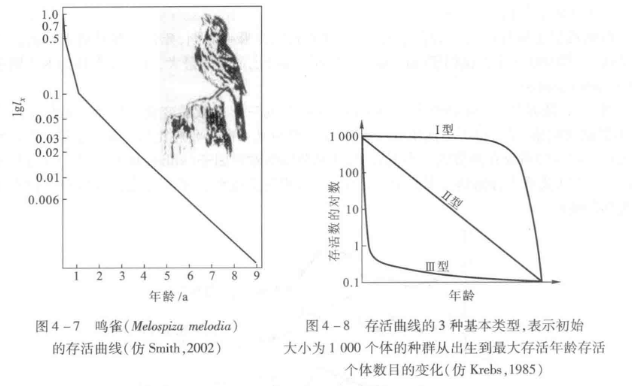
image.png

存活曲线直观地表达了同生群的存活过程。为了方便不同动物的比较，横轴的年龄可以各年龄期占总存活年限的百分数来表示。一般可将存活曲线分为如下3种基本类型（图4-8）：

  • I型：曲线凸型，表示幼体存活率高，而老年个体死亡率高，在接近生理寿命前只有少数个体死亡。如大型哺乳动物和人的存活曲线。
  • II型：曲线呈对角线型，表示在整个生活期中，有一个较稳定的死亡率。如一些鸟类中出现的模式。图4-7所示的存活曲线就是一个较为典型的鸟类存活曲线。在出生后很短的一段时间内，幼体死亡率很高，呈现III型模式，但1年后死亡率趋于稳定，为II型模式。
  • III型：曲线凹型，表示幼体死亡率很高，如产卵鱼类、贝类和松树的存活模式。

实际生活的大部分生物种群的存活曲线不是典型的存活曲线，但可表现出接近某种类型或中间型。大多数野生动物种群的存活曲线类型在II型和II型之间变化，而大多数植物种群的存活曲线则接近III型。伊藤(1980)在其《比较生态学》一书中认为随着动物进化从海洋进入陆地的过程，动物的产仔数量也按上述顺序减少，促使存活曲线由III型—II型—I型进化。——《基础生态学》pp.71-74

矩阵群体模型（Matrix Population Models，MPM）（生态学）

Matrix Population Models（矩阵种群模型）是一种强大的工具，用于研究种群动态，特别是当种群的个体按照年龄、生命阶段或空间分布分组时。这些模型在生态学中被广泛用于预测种群增长、了解种群对环境变化的响应、以及评估管理或保护措施的影响。

1. 模型基础

  • 矩阵种群模型基于离散时间步长。
  • 种群由多个状态组（如年龄组或生命阶段）构成。
  • 每个时间步中，个体可以：
  • 存活并留在当前组；
  • 过渡到下一个组；
  • 繁殖并产生新的个体进入第一个组。

2. 矩阵表示

矩阵模型的核心是一个投影矩阵（Projection Matrix，或称 Leslie Matrix），用来表示各状态组之间的转移关系。

假设种群分为 $n$ 个组，用向量表示每个组的个体数 $\mathbf{n}_t = [n_1, n_2, \dots, n_n]^T$，投影矩阵 $\mathbf{A}$ 表示每组之间的过渡关系：

$$
\mathbf{n}_{t+1} = \mathbf{A} \cdot \mathbf{n}_t
$$

矩阵 $\mathbf{A}$ 的形式通常为：

$$
\mathbf{A} =
\begin{bmatrix}
f_1 & f_2 & \cdots & f_n \\
s_1 & 0 & \cdots & 0 \\
0 & s_2 & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & s_{n-1}
\end{bmatrix}
$$

  • $f_i$：第 $i$ 组的繁殖率。
  • $s_i$：第 $i$ 组的存活率。

矩阵群体模型与生命表数据的互转

矩阵群体模型（Matrix Population Models）与生命表（Life Table）虽然在形式上不同，但都描述了种群在时间上的动态变化，且可以相互转换。

从生命表到矩阵群体模型

将生命表数据转化为矩阵群体模型的步骤如下：

（1）计算繁殖率 $F_i$

$$
F_i = l_i \cdot m_i
$$

  • $l_i$ ：年龄阶段 $i$ 的存活率。
  • $m_i$ ：年龄阶段 $i$ 的生殖率。

（2）计算阶段间存活概率 $P_i$

$$
P_i = \frac{l_{i+1}}{l_i}
$$

  • $l_{i+1}$ ：下一阶段的存活率。
  • $l_i$ ：当前阶段的存活率。

（3）构建勒斯利矩阵

将 $F_i$ 放在矩阵的第一行（繁殖率），$P_i$ 放在次对角线（阶段间存活率）。

从矩阵群体模型到生命表

如果已知转移矩阵 $\mathbf{A}$ ，可以反向推导生命表：

（1）计算存活率 $l_x$

  1. 假设种群初始分布 $\mathbf{n}(0)$，如 $\mathbf{n}(0) = [1, 0, 0, \dots, 0]$ （所有个体初始处于第一个年龄段）。
  2. 通过矩阵迭代计算种群分布： $\mathbf{n}(t) = \mathbf{A}^t \cdot \mathbf{n}(0)$
  3. 对每个阶段计算存活比例 $l_x$： $l_x = \frac{n_x(t)}{\text{初始种群规模}}$

（2）计算生殖率 $m_x$

从矩阵第一行 $F_i$ 和 $l_i$ 的关系反推出 $m_i$： $m_i = \frac{F_i}{l_i}$

生存分析（Survival Analysis）与生存曲线（Survival Curve）（临床医学）：

生存曲线是一种用来描述个体从某个时间点（如治疗开始）到某个事件发生（如死亡、疾病复发、痊愈等）之间的时间分布的图形。其数学方法包括参数法、半参数法和非参数法（如下图）。

image.png

两种常用方法

  1. Kaplan-Meier方法（KM曲线）：
    • 属于非参数法
    • 最常用的生存曲线绘制方法。
    • 以时间为横轴，生存概率为纵轴，通过统计每个时间点的生存率来绘制。
    • 常用于描述群体存活率的时间变化，并常用于两个不同处理的群体的比较研究。可以用直观的图形进行展示。
  2. Cox比例风险模型：
    • 属于半参数法
    • 用于分析多个变量（如年龄、治疗方法）对生存时间的影响。
    • 不直接绘制生存曲线，但可用于调整风险后生成生存曲线。

Kaplan-Meier生存曲线的绘制步骤

  • 数据准备：

    • 定义生存时间（time to event）：从起始点到事件发生或随访结束的时间。
    • 确定结局事件（event of interest）：例如死亡、疾病复发。
    • 区分完全数据（事件发生）和删失数据（事件未发生但随访结束）。

  • 计算生存率：

    • 事件发生概率（q）： 每个时间点的事件数 / 在风险中的总人数。
    • 生存概率（S）： 生存概率是累积的，计算公式为： S(t)=S(t−1)×(1−事件数/在风险人数)
    • 起始时间点的生存概率定义为 1（即 100% 存活）。

  • 绘制曲线：

    • 使用阶梯式的“阶梯函数”图（step function）。
    • 横轴为时间，纵轴为生存概率（S(t)）。
    • 事件发生时，曲线向下阶梯变化；删失点用竖线或符号标记。

下面我们以一个R语言代码实例介绍一下Kaplan-Meier生存曲线。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
### 1. 安装和加载R包
# 绘制Kaplan-Meier生存曲线需要用到的R包：survminer和survival。
# 如果没有安装就先安装。
install.packages("survminer") # 安装survminer包
install.packages("survival") # 安装survival包
library(survminer) # 加载包
library(survival) # 加载包

### 2. 导入内置数据集
# 使用survival包的lung数据集进行演示。
data(lung) # 加载lung数据集
head(lung) # 查看数据集。这个数据集的前6行如下：
##   inst time status age sex ph.ecog ph.karno pat.karno meal.cal wt.loss
## 1    3  306      2  74   1       1       90       100     1175      NA
## 2    3  455      2  68   1       0       90        90     1225      15
## 3    3 1010      1  56   1       0       90        90       NA      15
## 4    5  210      2  57   1       1       90        60     1150      11
## 5    1  883      2  60   1       0      100        90       NA       0
## 6   12 1022      1  74   1       1       50        80      513       0
# lung数据集：NCCTG晚期肺癌患者的生存率。
# inst # 机构代码；
# time # 生存天数；
# status # 生存状态，1为删失，2为死亡；
# age # 年龄；
# sex # 性别，1为男性，2为女性；
# ph.ecog、ph.karno、pat.karno # 为病人和患者评分，这里用不到；
# meal.cal # 进食时消耗的卡路里；
# wt.loss # 最近6个月内的体重下降。

### 3. 拟合生存曲线
## 3.1 创建生存对象
# 在survival包中先使用Surv()函数创建生存对象，生存对象是将事件时间和删失信息合并在一起的数据结构。
attach(lung) # 绑定数据集
Surv(time,status) # 创建生存对象
# 在上面输出的生存对象中，带"+"号的表示右删失数据。
## 3.2 拟合曲线
# R中使用survfit()函数来拟合生存曲线。
fit <- survfit(Surv(time,status) ~ sex,  # 创建生存对象 
               data = lung) # 数据集来源
fit # 查看拟合曲线信息
## Call: survfit(formula = Surv(time, status) ~ sex, data = lung)
## 
##         n events median 0.95LCL 0.95UCL
## sex=1 138    112    270     212     310
## sex=2  90     53    426     348     550

### 4. 绘制曲线+中位生存时间+置信区间
ggsurvplot(fit, data = lung,
           surv.median.line = "hv",  # 增加中位生存时间
           conf.int = TRUE) # 增加置信区间

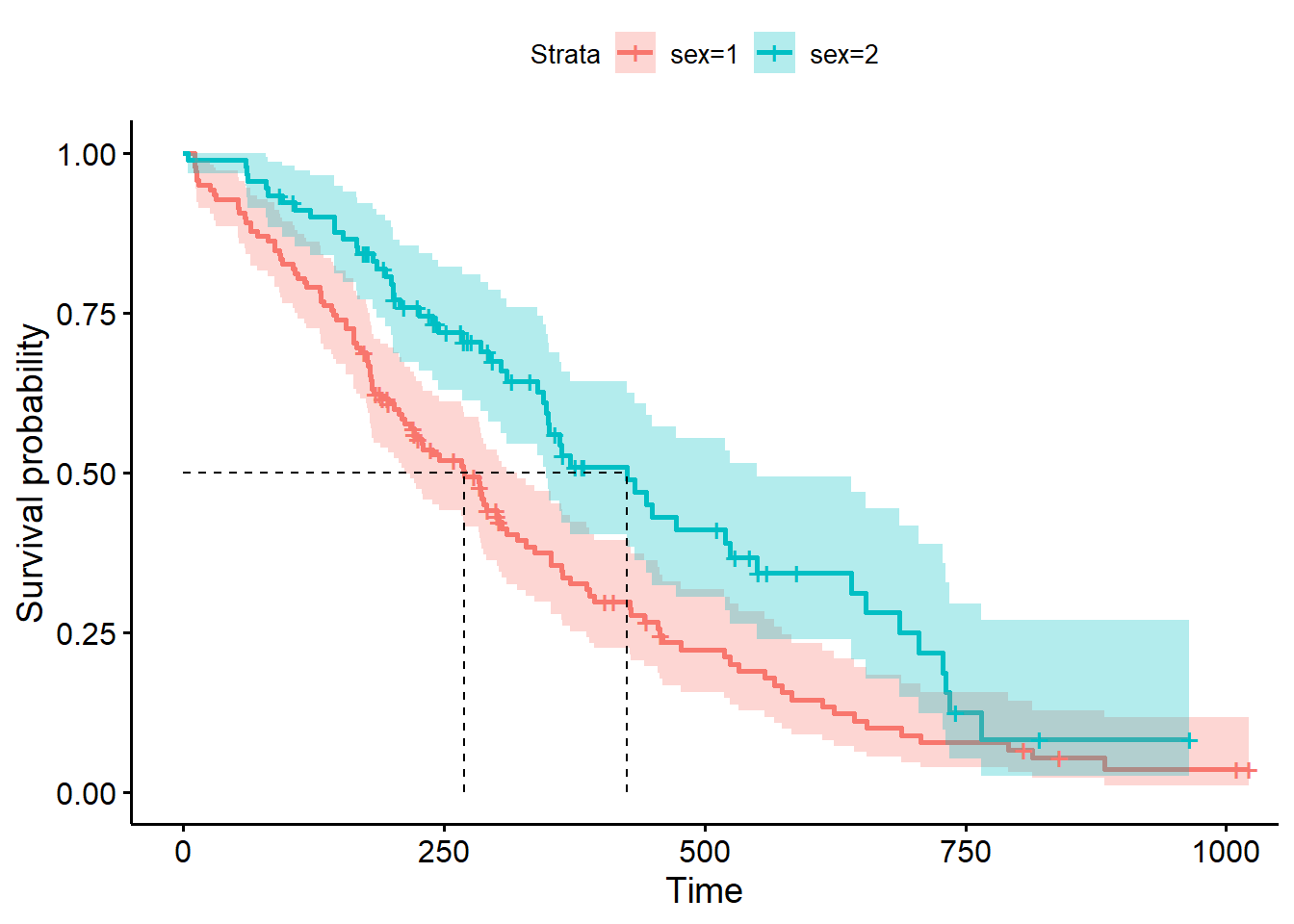
从 fit 的输出可以得知，lung数据集中的样本包含138例男性和90例女性；男性和女性发生感兴趣结局事件（包括死亡和删失）分别有112例和53例。男性和女性的中位生存时间分别为270天和426天。

上面的代码最终绘制出的结果图（KM曲线）如下图。两条曲线分别显示了两种性别患者的生存率随时间的变化。

中位生存时间(median survival time)又称为生存时间的中位数，表示刚好有50%的个体其存活期大于该时间，是生存分析中常用的概括性统计量。图解法是计算中位生存时间的方法，其利用生存曲线图，从纵轴生存率为50%处画一条与横轴平行的线，并与生存曲线相交，然后自交点画垂线与横轴相交，此交点对应的时间即为中位生存时间（如下图虚线）。可以看出，在lung数据集中，男性患者（sex=1）的中位生存时间低于女性患者（sex=2）。

Untitled.png

关于删失数据（Censoring）的一点讨论

在生存分析中，删失数据指在研究结束前，研究对象未发生感兴趣事件的情况，包括：

  • 右删失（Right Censoring）： 在随访期结束时，事件未发生。
  • 左删失（Left Censoring）： 事件发生在观察期开始之前（较少用）。
  • 区间删失（Interval Censoring）： 事件发生的确切时间未知，只知道发生在某个时间区间内。

其中，右删失最常见，例如，在癌症患者的生存分析中，一部分患者在研究结束时仍存活，但无法继续随访。这些患者的数据被视为右删失。在 Kaplan-Meier 方法中，通过如下策略处理删失数据：

  1. 删失点的标记： 在生存曲线上标出删失的时间点（通常用竖线或其他符号表示）。
  2. 删除删失患者后重新计算：
    • Kaplan-Meier 方法计算每个时间点的生存概率时，仅基于该时间点仍在研究中的受试者。
    • 如果时间点 $t_i$ 有 $d_i$ 人发生事件且 $n_i$ 人仍在研究中，则生存概率为 $S(t_i) = S(t_{i-1}) \times \left(1 - \frac{d_i}{n_i}\right)$
    • 删失患者只影响 $n_i$ 的值，但不直接改变生存概率。

另外，生态学中的生命表和生存曲线中，也有类似删失数据的处理情况。不过生态学通常更注重总体趋势，不刻意标注删失：一些生命表将这些个体视为右删失（未能完整跟踪其生命状态）；另一些则选择忽略这些个体对生存概率的影响。