计算生物学部分知识点整理
来自最近的助教课备课笔记。主要涉及两部分内容:生物节律检测,以及系统发育分析(包括序列比对和建树算法)。
一、生物节律
(一)生物节律的研究背景
昼夜节律(Circadian Rhythms)指的是身体在 24小时 内经历的身体、心理和行为变化的自然循环。
- 它是一种 内源性的节律 ,会影响睡眠、体温、激素、食欲和其他身体功能。
- 昼夜节律主要受光和暗的影响,并由大脑中部的一个小区域控制。
- 昼夜节律异常可能与肥胖、糖尿病、抑郁症、双相情感障碍、季节性情感障碍和失眠等睡眠障碍有关。
- 昼夜节律有时被称为“生物钟”
2017年的诺贝尔生理学和医学奖授予了Jeffrey C. Hall、Michael Rosbash和Michael W. Young,以表彰他们对生物昼夜节律分子机制的研究 。1984年,Jeffrey和Michael合作克隆了控制果蝇昼夜节律的基因,即period基因(per),其编码的PER蛋白水平在夜晚积累,在白天降解,呈现出24小时的周期性变化。1994年,Michael W. Young发现了另一个与昼夜节律相关的基因,即timeless基因(tim),其编码的TIM蛋白与PER蛋白相互作用,共同调节生物钟。
另外这里分享一篇论文:
Young, Michael W. “Time Travels: A 40-Year Journey from Drosophila’s Clock Mutants to Human Circadian Disorders (Nobel Lecture).” Angewandte Chemie (International ed. in English) vol. 57,36 (2018): 11532-11539. doi:10.1002/anie.201803337
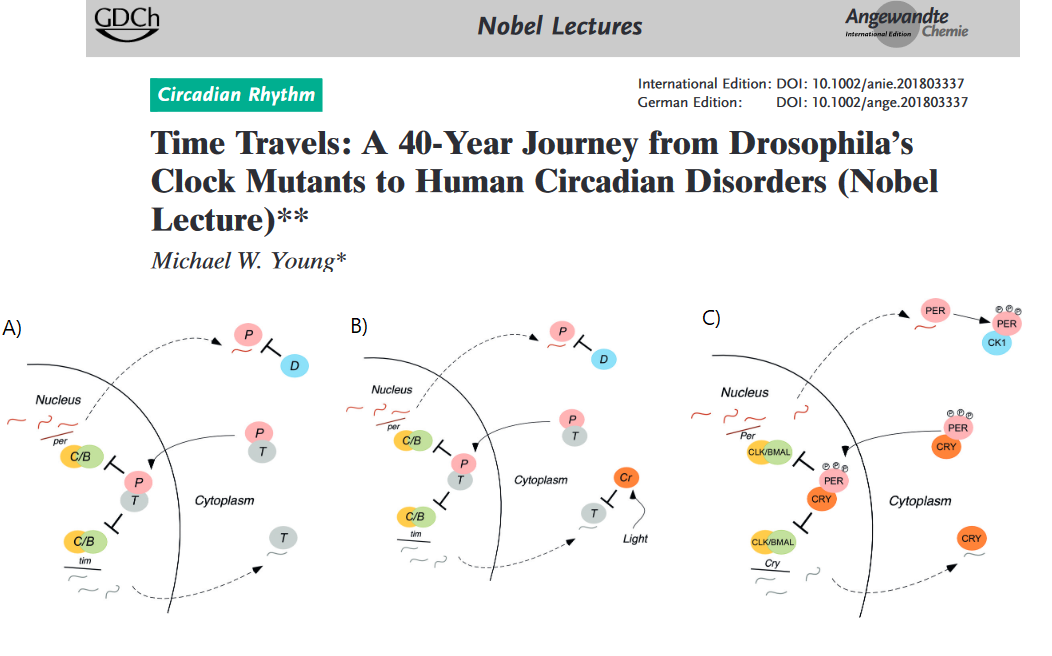
这篇文章(Michael Young等),主要讲了果蝇和人类当中的节律调控系统,以及隐花色素(Cry)上的突变与睡眠周期障碍的关联。
首先是Michael Young等人最初在果蝇里面筛选到了几个重要的突变体:Period(PER)、Timeless(TIM)、dClock(dCLK)、Cycle(CYC),其中在全暗环境下,最初缺乏PER/TIM二聚体,此时dCLK和CYC会发挥转录因子活性,驱动PER和TIM表达;随着时间积累,PER/TIM二聚体,反过来抑制dCLK和CYC活性。随着PER/TIM水平降低(被降解),dCLK和CYC的活性会再次出现,如此往复形成循环(A图)。
在果蝇当中,还存在两个重要的调控蛋白:Doubletime(DBT)和Cryptochrome(隐花色素,CRY)。前者抑制单体状态下的PER,导致周期延长;后者在有光照的条件下抑制TIM,同样导致周期延长(B图)。
在人类当中,没有TIM蛋白,隐花色素CRY此时充当了TIM的角色(而失去了光感受器的功能)。其他蛋白则如常(C图)。
跨时区旅行“倒时差”行为促进了不同器官的节律周期非同步调相的研究。而对于一种睡眠障碍(Delayed sleep phase disorder,DSPD)的家系研究,在CRY基因上定位到了几个突变,影响了生物时钟节律的调整与同步。
(二)检测生物节律信号的数学原理
谐波回归(Harmonic Regression)
谐波回归(Harmonic Regression)是一种统计技术,通过结合周期函数(特别是正弦和余弦项)来扩展传统回归分析,以对时间序列数据中的周期性模式进行建模。通过最小化下列公式的AICc值,从而实现参数的最优化。
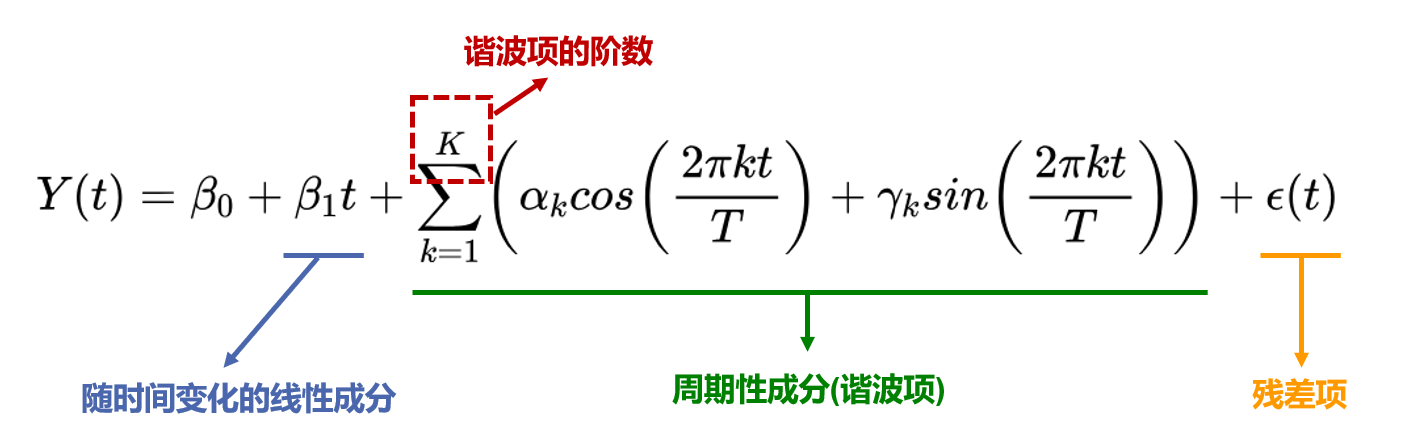
优点
- 允许任何长度的周期
- 对于复杂的时间序列数据,可以纳入多个不同频率的谐波项以更好地拟合
缺点
- 假设周期固定,可能并不适用于所有数据集。
- 此外,如果包含太多谐波项,谐波回归可能会变得过于复杂,导致过度拟合
JTK_cycle
JTK_cycle是Karl Kornacker和John Hogensch教授合作开发的非参数算法。其目的是识别大型基因组规模数据集中的节律成分,并估计其周期长度、相位和振幅。

通过计算时间序列数据与不同周期长度和相位的余弦波形之间的相关性,来判断是否存在周期性变化以及周期性变化的参数。使用Kendall’s S 统计量进行非参数的统计检验
优点:可以区分振幅较小的周期模式,特异性和灵敏性高,对异常值的容抵抗力高;在大数据计算中,速度比较快。
缺点:余弦拟合类算法的固有问题(不能识别出非固定周期的信号;较难识别非正弦波信号);
另外可以参考以下论文和代码实现:
Hughes ME, et al. J Biol Rhythms(2010).doi:10.1177/0748730410379711
https://openwetware.org/wiki/HughesLab:JTK_Cycle
https://openwetware.org/wiki/File:JTKversion3.zip
RAIN算法
RAIN(Rhythmicity Analysis Incorporating Non-parametric Methods)也是一种非参数检验的方法,但原理和JTK_Cycle有所不同,它是通过按时间点(如昼夜节律或时间段)对测量值进行分组来工作。用于统计检验的是数据点的rank而不是value,并将各组数据点与上升模式和下降模式的替代假设( $H_A$ )进行比较。只有属于相同模式(上升或下降)的群体才会相互比较。这拓宽了对波形的许多限制,允许检测例如“鱼翅”波等不同波形。通过循环重新排序组,并通过进一步改变伞形峰位置,可以进一步测试不对称性和相位。
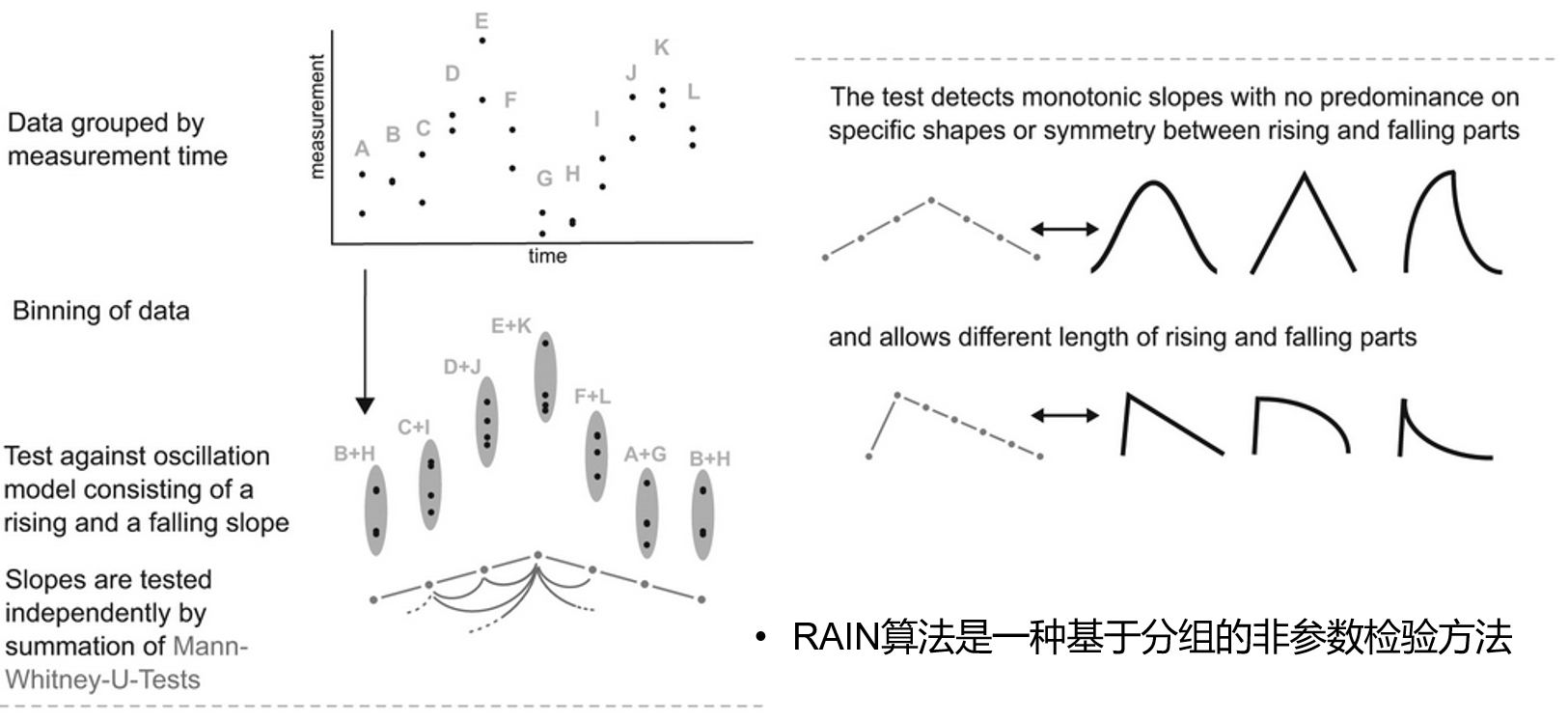
另外参考:
https://rdrr.io/bioc/rain/
Thaben PF, Westermark PO. Journal of Biological Rhythms(2014). doi:10.1177/0748730414553029
ARSER
ARSER是一种基于自回归谱(autoregressive spectral, AR)的分析方法。在自回归模型中,我们基于目标变量历史数据的组合对目标变量进行预测。所谓自回归,“自”字即表明其是对变量自身进行的回归。其使用多个历史数据去预测当前数据,Φ1,Φ2,……的不同组合会造就不同的周期模式。
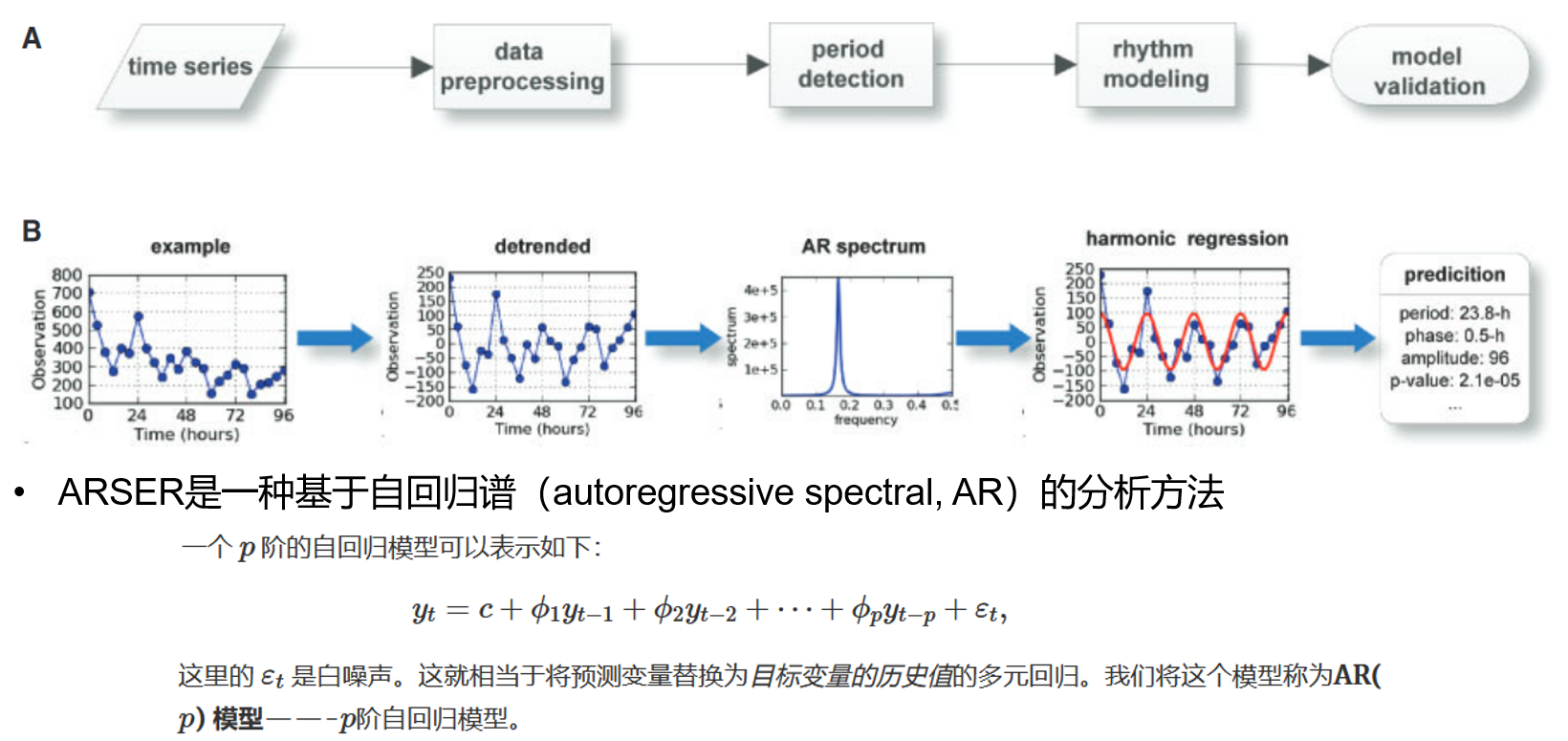
另外参考:
Rendong Yang, Zhen Su. Bioinformatics(2010). doi:10.1093/bioinformatics/btq189
https://otexts.com/fppcn/AR.html
傅里叶变换和小波变换(Fourier transform and Wavelet transform)
如图。
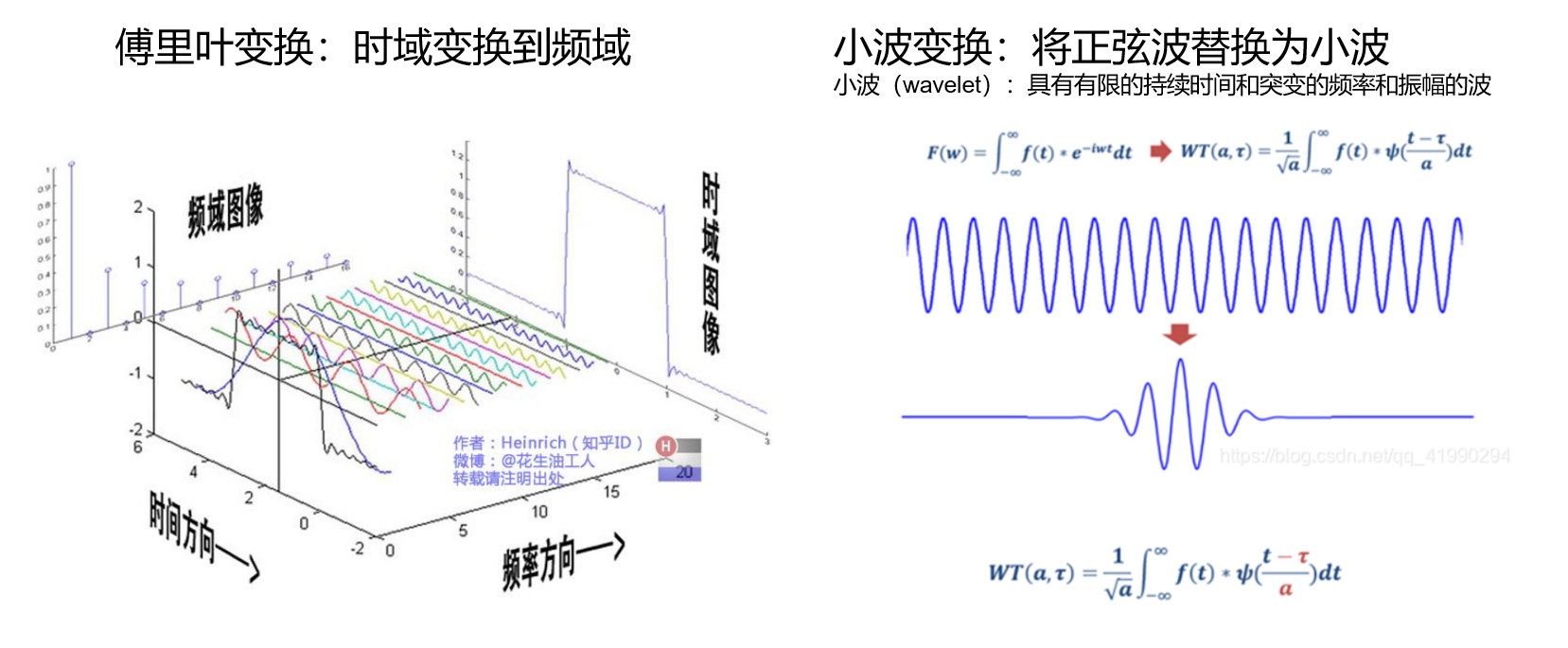
傅里叶变换是将信号从时域到频域的变换,其假设信号是由不同周期的正弦波叠加形成。
由于日常生活中的信号并不是一直光滑的,而且奇异点是平凡的,傅立叶在奇异点的表现很糟糕(会产生Gibbs效应,即在信号突变的位置出现明显的振荡),因此小波变换应运而生。所谓小波(wavelet)指的是具有有限的持续时间和突变的频率和振幅的波,其有许多不同种类,可以用于对不同类型的信号进行小波变换。
另外参考:
https://zhuanlan.zhihu.com/p/19763358
https://www.cnblogs.com/jfdwd/p/9249850.html
MetaCycle:一个用于检测生物节律信号的R包
MetaCycle包主要用于从大规模时间序列数据中检测节律信号。根据每个时间序列数据的特征,MetaCycle内置了ARSER(ARS)、JTK_CYCLE(JTK)和Lomb Scargle(LS)等算法,进行周期性信号检测。

另外参考:
https://rdrr.io/cran/MetaCycle/f/vignettes/implementation.Rmd
https://github.com/gangwug/MetaCycle
二、系统发育分析与建树算法
系统发育进化树 (Phylogenetic tree):一般也叫系统进化树,进化树。它可以利用树状分支图形来表示各物种或基因间的亲缘关系。
分支系统发育分析 (Molecular phylogenetic analysis):是用来研究物种或序列进化和系统分类的一种方法。一般研究对象是碱基序列或氨基酸序列,通过数理统计算法来计算生物间进化关系。最后,根据计算结果,可视化为系统进化树。
系统发育分析的大致流程一般如下:
- (1) 选择需要分析的序列(selection of sequences for analysis)
- (2) 多重序列比对(multiple sequence alignment,MSA)
- (3) 进化模型的确定(specification of a statistical model of evolution)
- (4) 构建系统发育树(tree building)
- 基于距离的建树方法(Distance-based method):e.g. UPGMA, NJ
- 最大简约法(Maximum parsimony method)
- 最大似然法(Maximum likelihood method)
- 贝叶斯方法(Bayesian inference method)
- (5) 系统发育树的评估(tree evaluation)与下游分析
(一)两条序列之间的比对
序列比对大致分为下面几种:
- 全局比对(Global alignment):
- 序列全长的比较,旨在揭示序列间的整体相似性和差异性。
- 如:两个基因的比对。
- 半全局比对(Semi-global alignment):
- 用一条短序列比对另一条长序列。
- 如:数据库搜索。
- 局部比对(Local alignment):
- 寻找整条序列上比对最好(相似度最高)的局部区域。
- 如:两条基因组之间的比对。
动态规划法是序列比对的常用方法,其大致原理如下:
第一步,打分。将两条序列分别写在打分矩阵的横行和纵列上。左上角单元格的初始值赋值为0,从这个单元格开始,基于给定的打分系统,向右、下、右下三个方向进行打分。
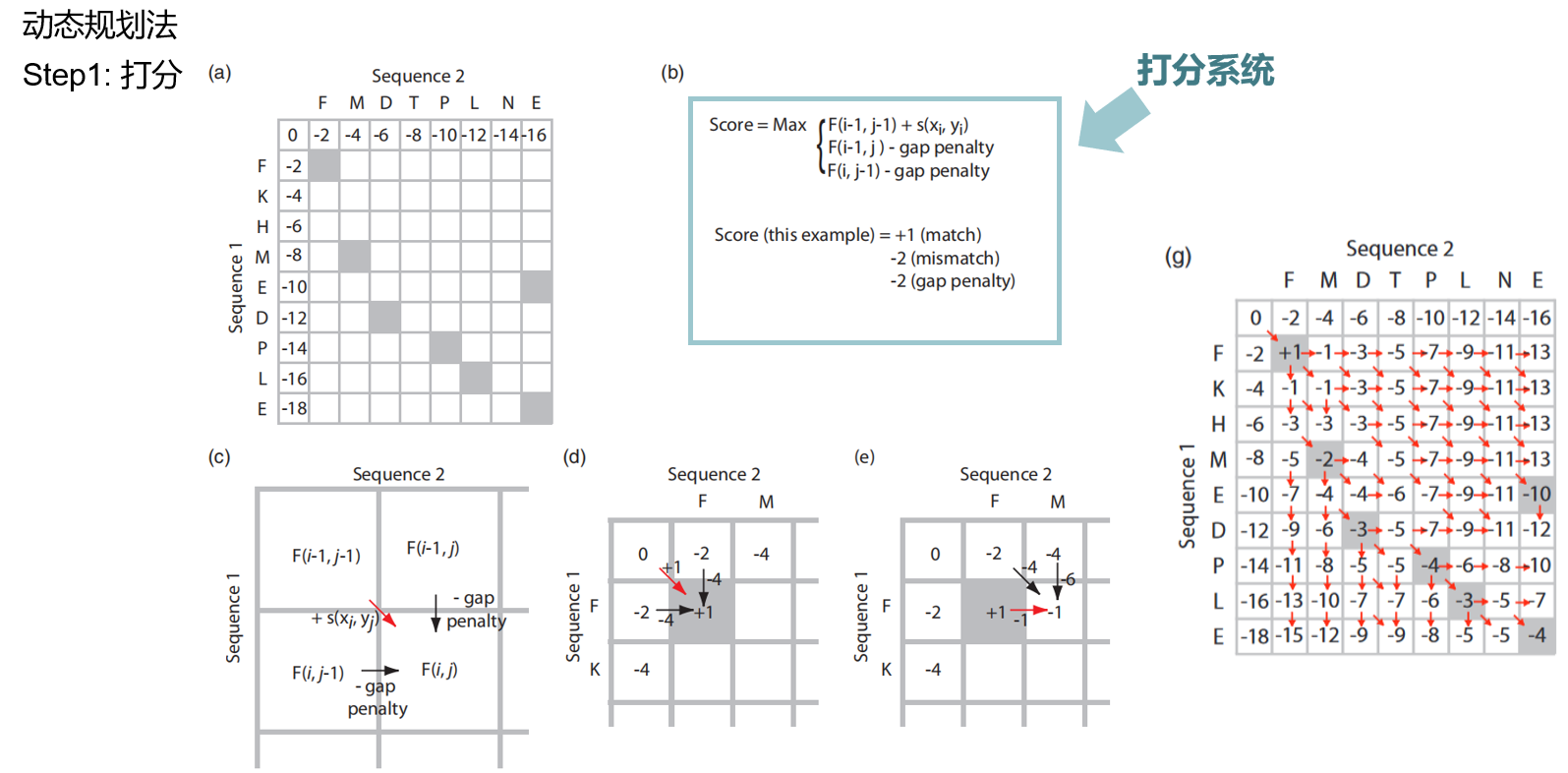
第二步,回溯。从右下的单元格开始往左上回溯,回溯的方向取决于当前单元格中的score来自哪一个方向(例如,如果当前单元格中的分数是从左上方单元格+1 match来的,则回溯方向是左上;如果当前单元格中的分数是从左侧单元格+1 gap来的,则回溯方向是左。当分数有多个来源时,代表存在多条可行的回溯路径)。根据回溯路径,我们就可以写出序列比对的结果。
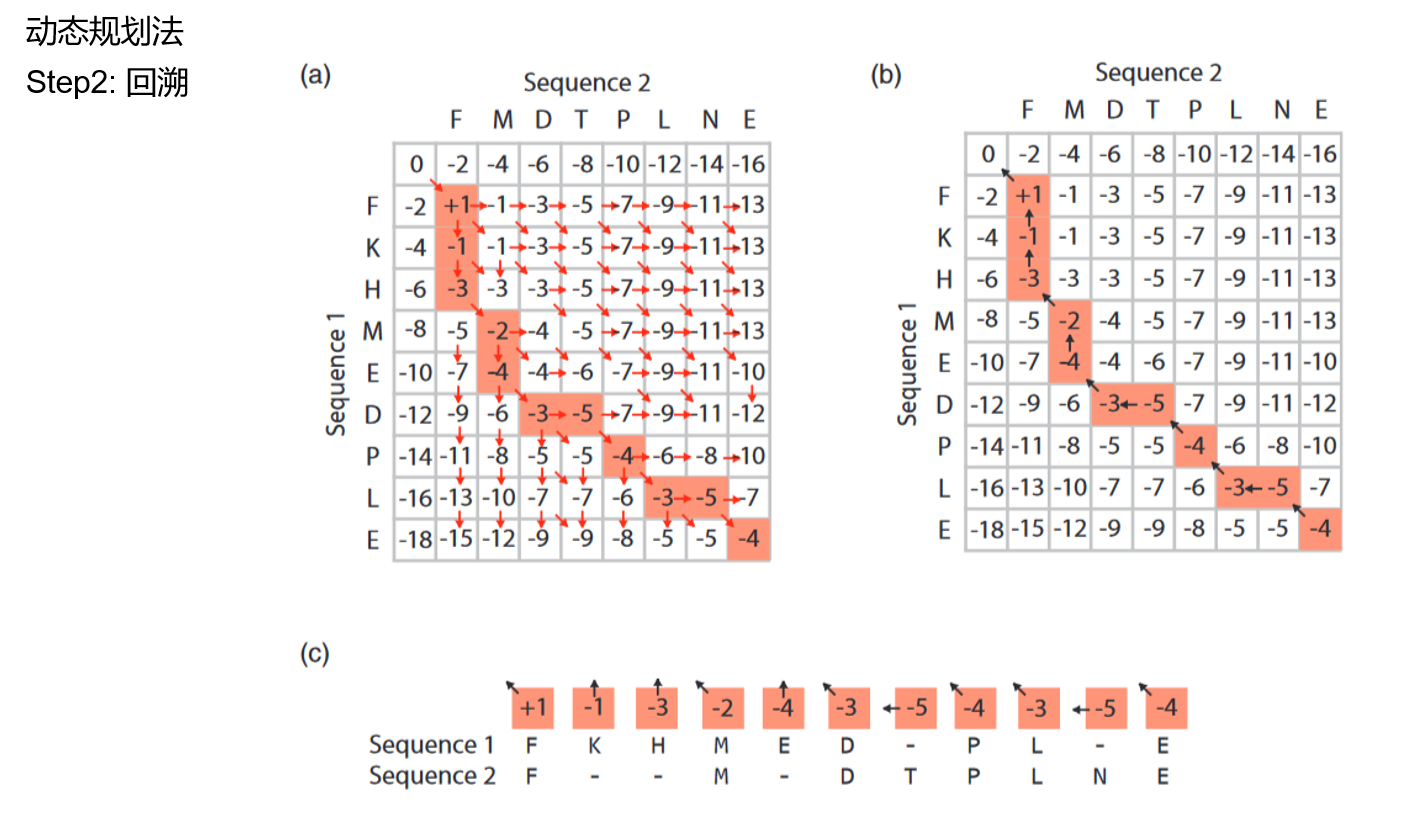
用于序列比对的动态规划算法包括Needleman and Wunsch algorithm和Smith and Waterman algorithm等,其中前者用于全局比对,后者用于局部比对。二者的差异主要在于,局部比对的打分系统不允许负值分数的存在;如果一个单元格的分数从三个方向上看都小于0,则将这个单元格的分数赋值为0。

此外,针对序列比对时空位出现位置不连续的问题,有两个tricky的手段:仿射空位罚分和Gotoh算法,其具体原理如下图所示:

(二)多重序列比对
最简单粗暴的多重序列比对方法就是直接比对,构建一个高维的打分矩阵,然后用动态规划的思路去寻找最优的比对路径。然而这种方法的缺点在于时间复杂度过高 ( $O(2^NL^N)$ ,$N$ 是序列数量,$L$ 是平均序列长度,下同 )。因此,需要一些更高效的方法。

ClustalW等软件采用了一种渐进式(“progressive”)的比对策略,首先在序列之间进行两两比对并构建进化距离矩阵,这个进化距离矩阵将用于构建一颗前导树(guide tree),之后ClustalW会基于这棵先导树进行多重序列比对结果的构建。时间复杂度更低,为 $O(N^4L^2)$ 。然而,渐进式比对策略具有一些局限性,例如一旦比对过程中出现错误,就无法纠正。

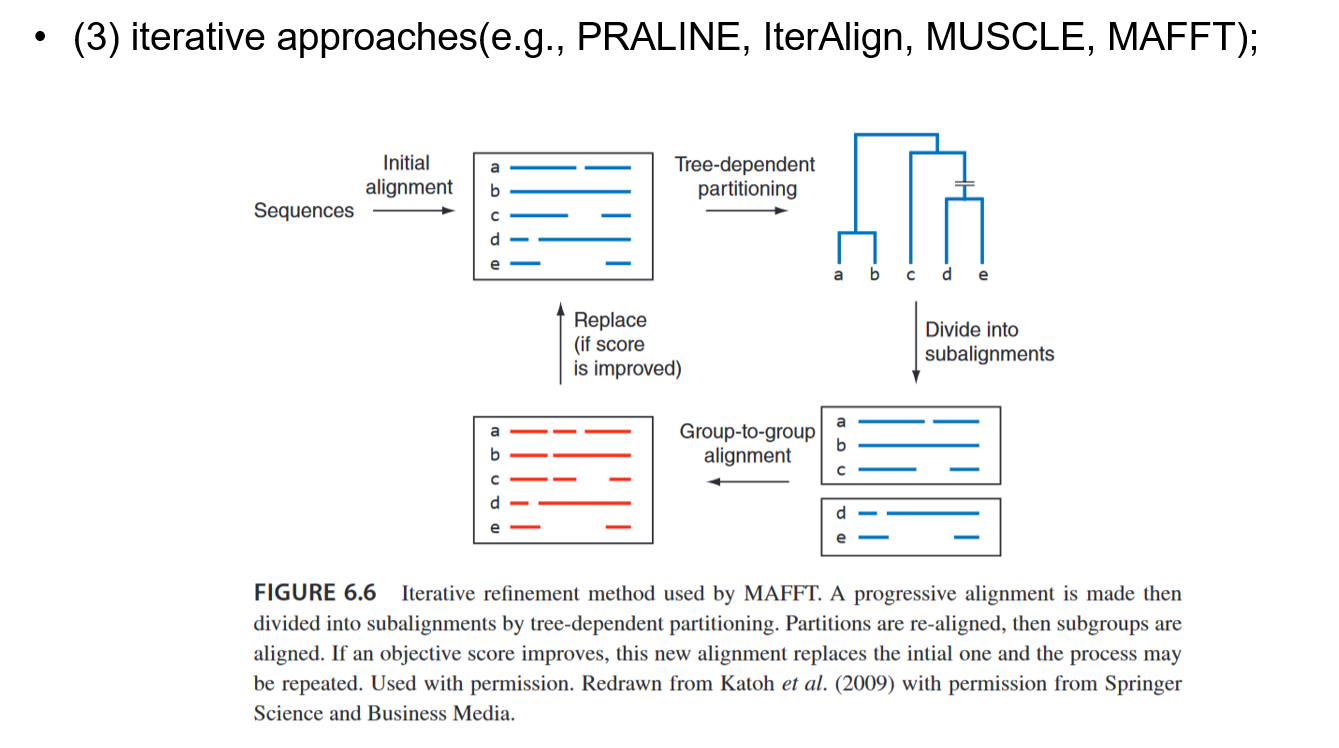
MAFFT等软件则更进一步,采用了一种迭代策略进行更精细的比对方法。首先,基于渐进式的比对策略创建一个初始比对,然后通过逐轮迭代对其进行改进,使用一些目标函数来最大化分数。渐进式比对策略一旦比对过程中出现错误,就无法纠正,而迭代策略可以很好的克服这一点。目前MAFFT是最常用的多重序列比对软件之一。
(三)建树算法
UPGMA法
UPGMA=“Unweighted pair group method with arithmetic mean”,这是一种基于进化距离的建树方法。其计算原理和过程如下:
- ①以已求得的距离系数,所有比较的分类单元的成对距离构成一个
t×t方阵,即建立一个距离矩阵M。 - ②对于一个给定的距离矩阵,寻求最小距离值
Dpq。 - ③定义类群p和q之间的分支深度
Lpq=Dpq/2。 - ④若p和q是最后一个类群,侧聚类过程完成,否侧合并p和q成一个新类群r。
- ⑤定义并计算新类群r到其他各类群
i(i≠p和q)的距离Dir=(Dpi+Dqi)/2。 - ⑥回到第一步,在矩阵中消除p和q,加入新类群r,矩阵减少一阶,重复进行直至达到最后归群。
UPGMA法比较直观和简单,运算速度快,应用很广。它的缺点在于当分子进化速率差异较大时,在建树过程会引入系统误差。

NJ法
NJ=“Neighbor-joining”,同样也是一种基于进化距离的建树方法。
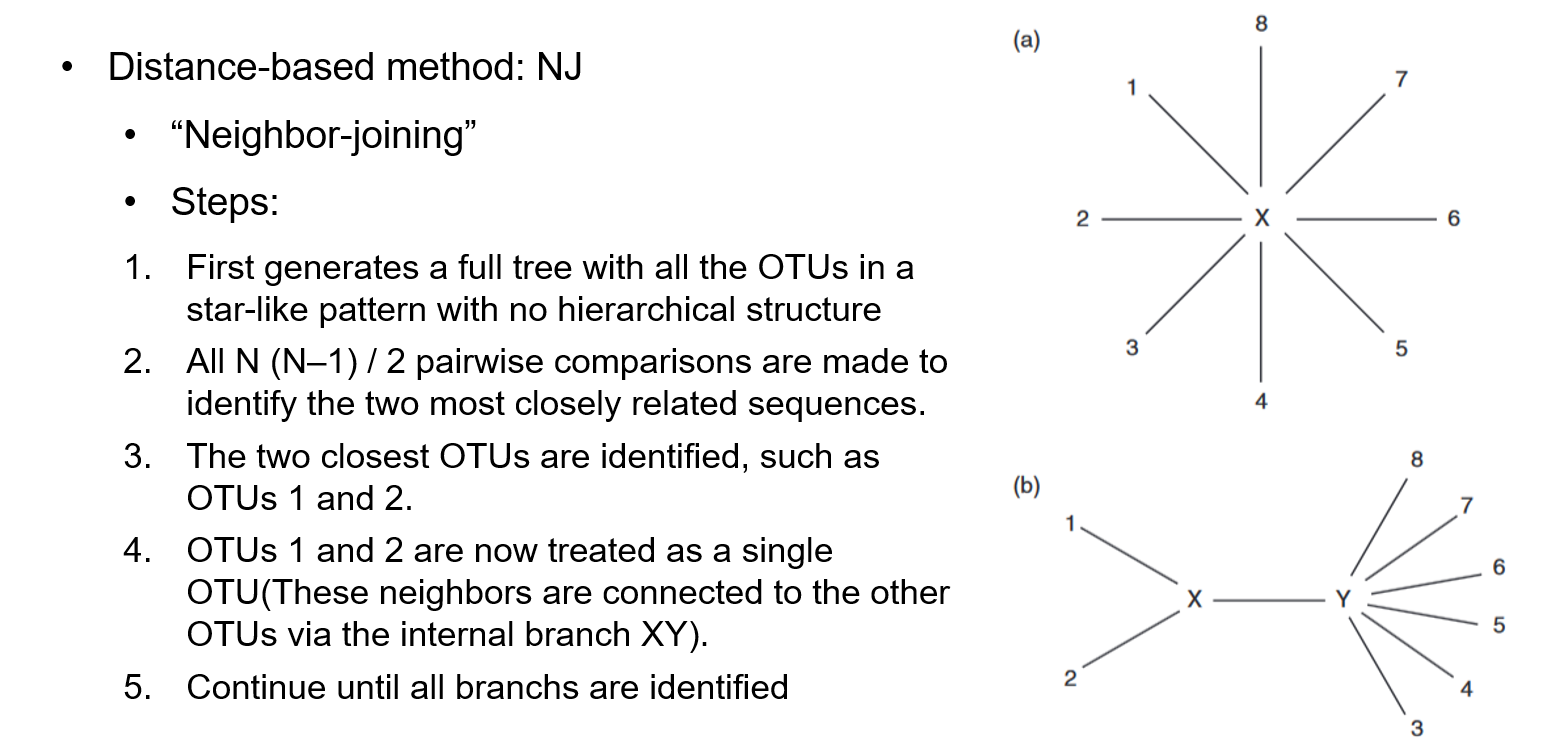
NJ法的具体计算过程如下图所示。相比于UPGMA法,NJ法主要有两点不同:
- (1)NJ法是从一棵星型树开始,逐步添加中间节点(自顶向下),而UPGMA法是从单独的叶子节点开始逐步构树(自底向上);
- (2)在计算过程中,使用校正后的进化距离矩阵 $M$ 代替原始的进化距离矩阵,其中
M(i,j)=d(i,j)-(r(i)+r(j))/(n-2)这个步骤是在矫正不同分支上进化速率的误差。因此,对于亲缘关系较远的物种,NJ法比UPGMA法的适应性更好。

最大简约法
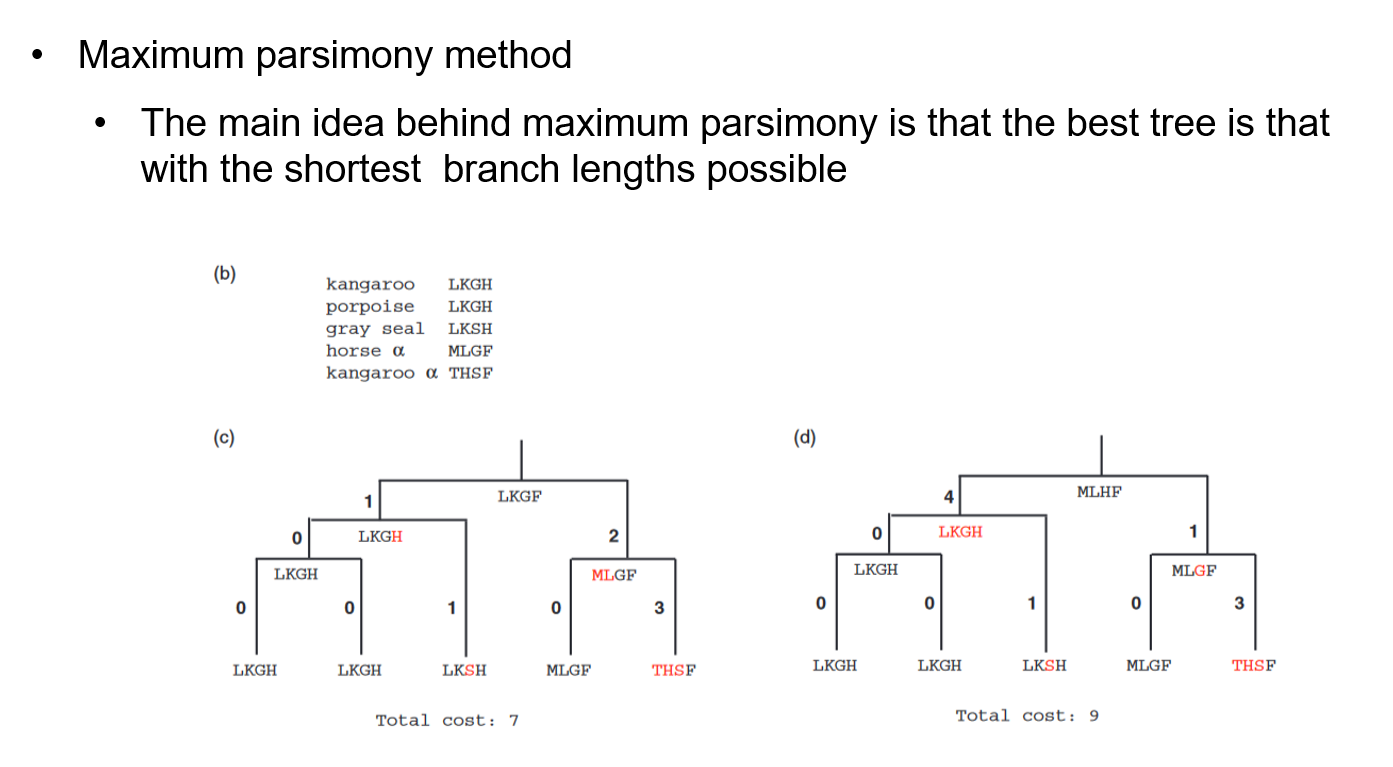
最大简约背后的主要思想是,最好的树是分支长度尽可能短的树(Czelusniak等人,1990)(这里的分支长度可以用突变数来表示)。
根据最大简约理论,用较少的变化来解释一组序列的进化方式比更复杂的分子进化解释更可取。因此,我们寻求对观测数据的最简约的解释。
最大简约法的原理就是尽可能地穷举所有可能的树形,并计算树上的总突变数。总突变数最少的树形将被看作是最优树形。
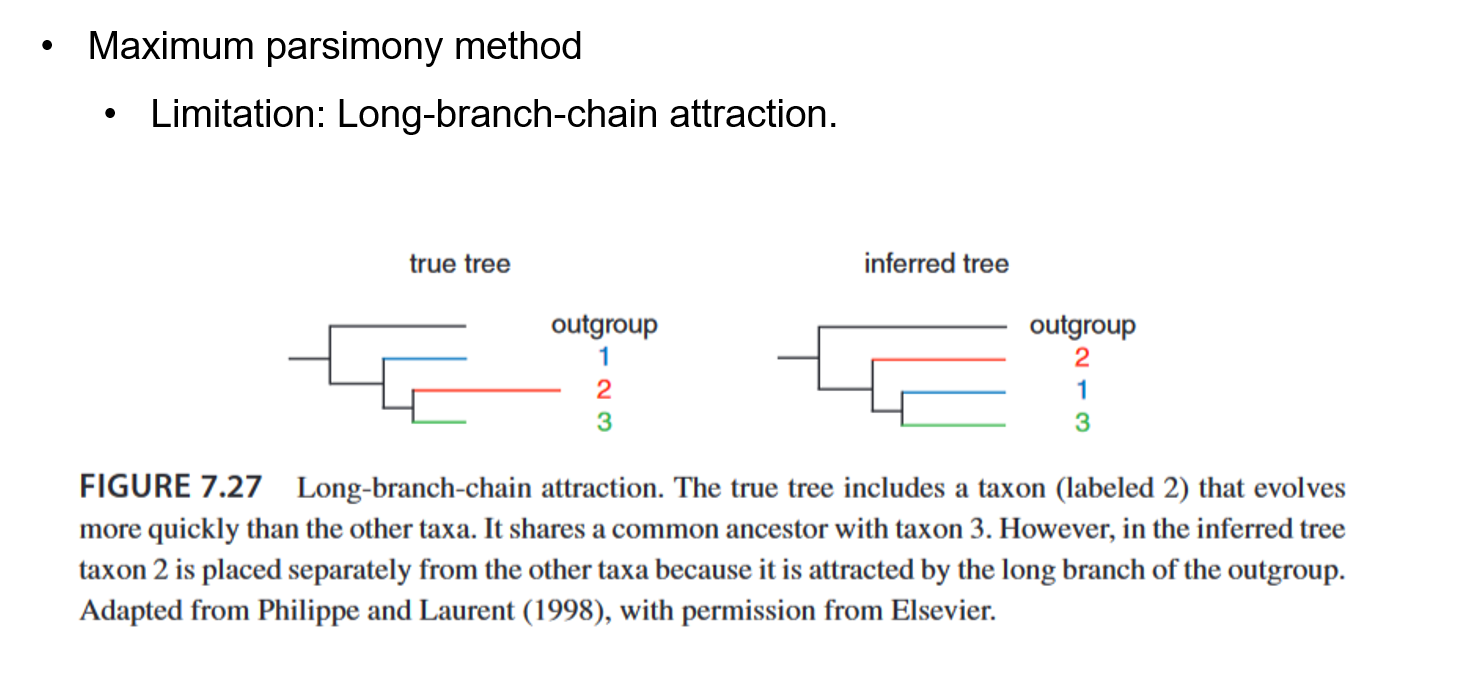
缺点:长枝吸引问题。由于最大简约法倾向于选择碱基替换数最少的进化树结构,就会错误的把一些长枝分类到外群上,或者错误将趋同/平行进化推断为同源。
对于最大简约法,也有一些tricky的手段以加快计算速度,如下:

最大似然法
如图。
这种方法基于概率模型进行推断,计算量最大,但也最为精准。

步骤如下:
