RNA-seq数据的归一化

发表于 分类于

这一篇教程节选自第一次助教课的课程内容。上周末准备助教课花了不少时间，也顺带复习了RNA-seq数据分析流程的相关知识。

背景：为什么要做RNA-seq的归一化

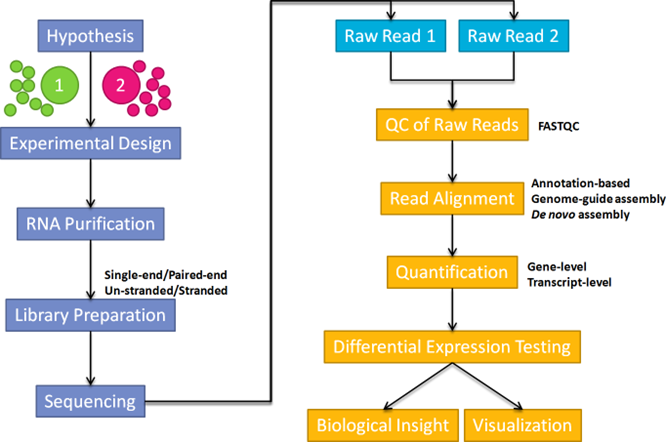
如下图所示，基于RNA-seq的差异表达研究的一般流程包括实验设计、RNA纯化、文库制备、测序以及下游分析等步骤。不同测序运行之间产生的读取数量存在很大差异，文库制备方案、测序平台和核苷酸组成也会带来许多技术偏差。要获得真实有效的科学发现，需要排除上面这些因素带来的偏差，而标准化（normalization）就是这样的一个过程。标准化旨在准确比较样本之间的基因表达。

image.png

影响标准化的三个因素

参考： 《跟着刘小泽一起回顾标准化方法》

三大因素如下：

  • 测序深度（Sequencing depth）
  • 基因长度（Gene length）
  • RNA组成（RNA composition）

测序深度

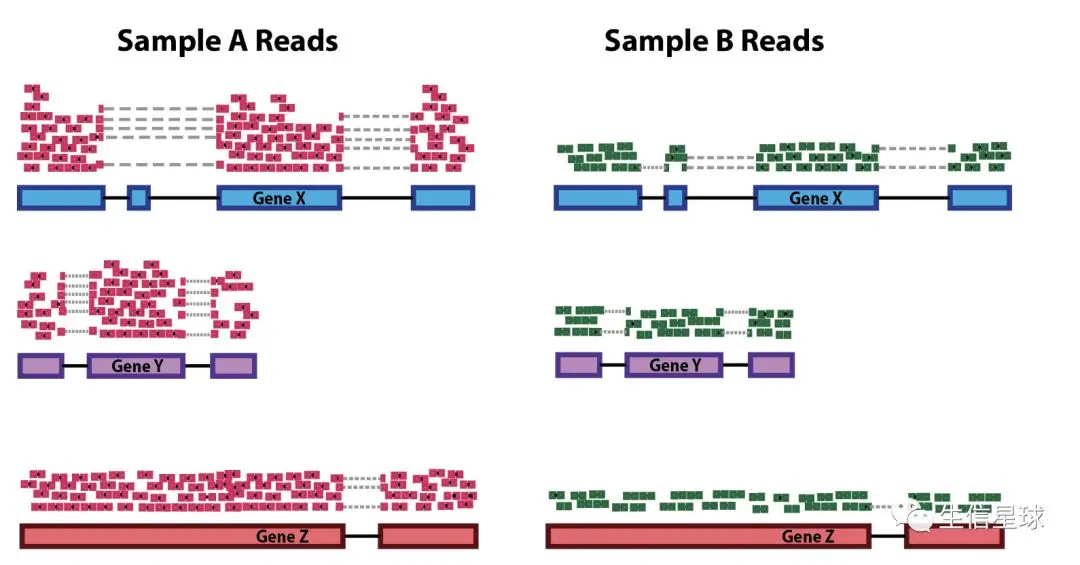
如果要比较两个样本的同一个基因表达量，那么首先要保证外部因素一致，最直接的体现就是测序深度。不同批次的测序，它的测序深度可能不同，因此可能导致下图这种情况。

如图所示，图中所有红色和绿色的小长条就是比对到基因的测序read，我们也是按它们的数量来判断某个基因表达量的；看到有的长条之间连了一条虚线，这表示它是跨越内含子比对的测序read。从图上看，貌似A样本的所有基因表达量都是B的两倍。

然而，实际情况下我们会遵循这样的一个前提假设，即不同样本当中绝大部分基因的表达量是不存在差异的，因此图中这种差异更有可能是测序深度导致的不同，例如sample A测了20x，但是sample B只测了10x，那么定量以后的raw count就有可能是图中这个样子，这种偏差当然要排除。排除这个因素的方法也很简单，用各个基因的reads除以对应sample的总reads就行（这也就是CPM矫正方法的原理）。

2024-06-17-144535.webp

基因长度

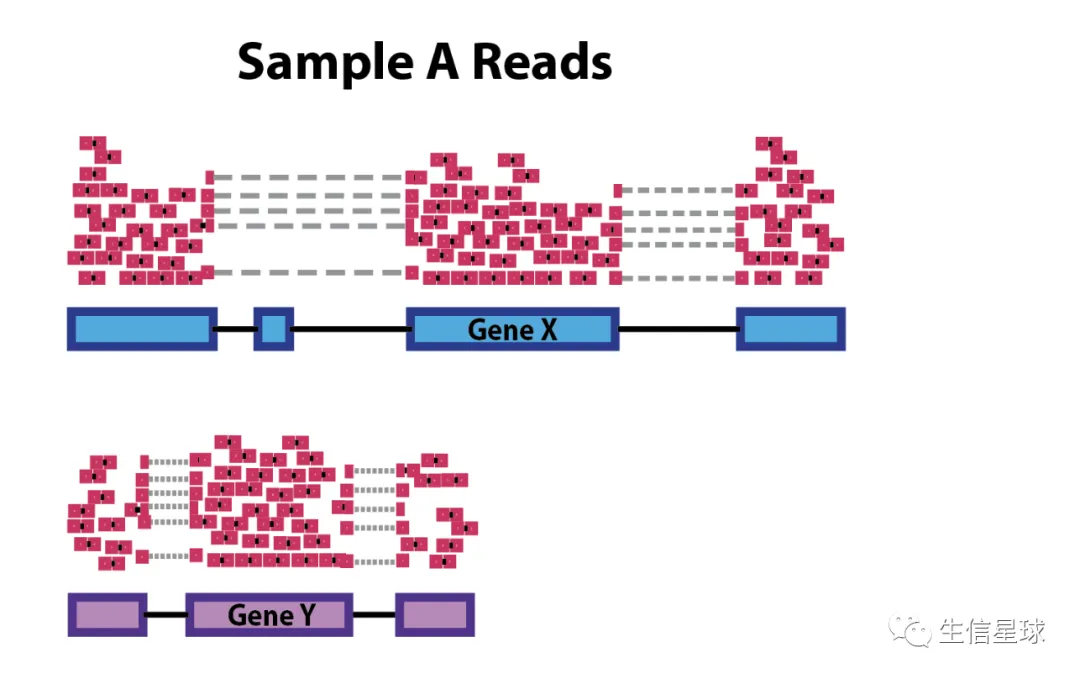
如果要比较同一个样本中的不同基因，那么就要处理好“内部矛盾”——基因长度的问题。基因的长度是固定的，如果要比较的两个基因中，一个基因本身就很长，那么理所应当，落在上面的reads数量应该也越多。因此可能导致下图这种情况，例如虽然都是sample A的基因，且从图中我们能感觉到基因X和Y的表达水平应该差不多，然而基因X比Y要长，也有更多的reads落在基因X上，这就会导致在做统计检验时很有可能会错判基因X表达量更高。

排除这个因素的方法也很简单，用各个基因的reads除以对应的基因长度即可。

2024-06-17-144544.webp

RNA组成

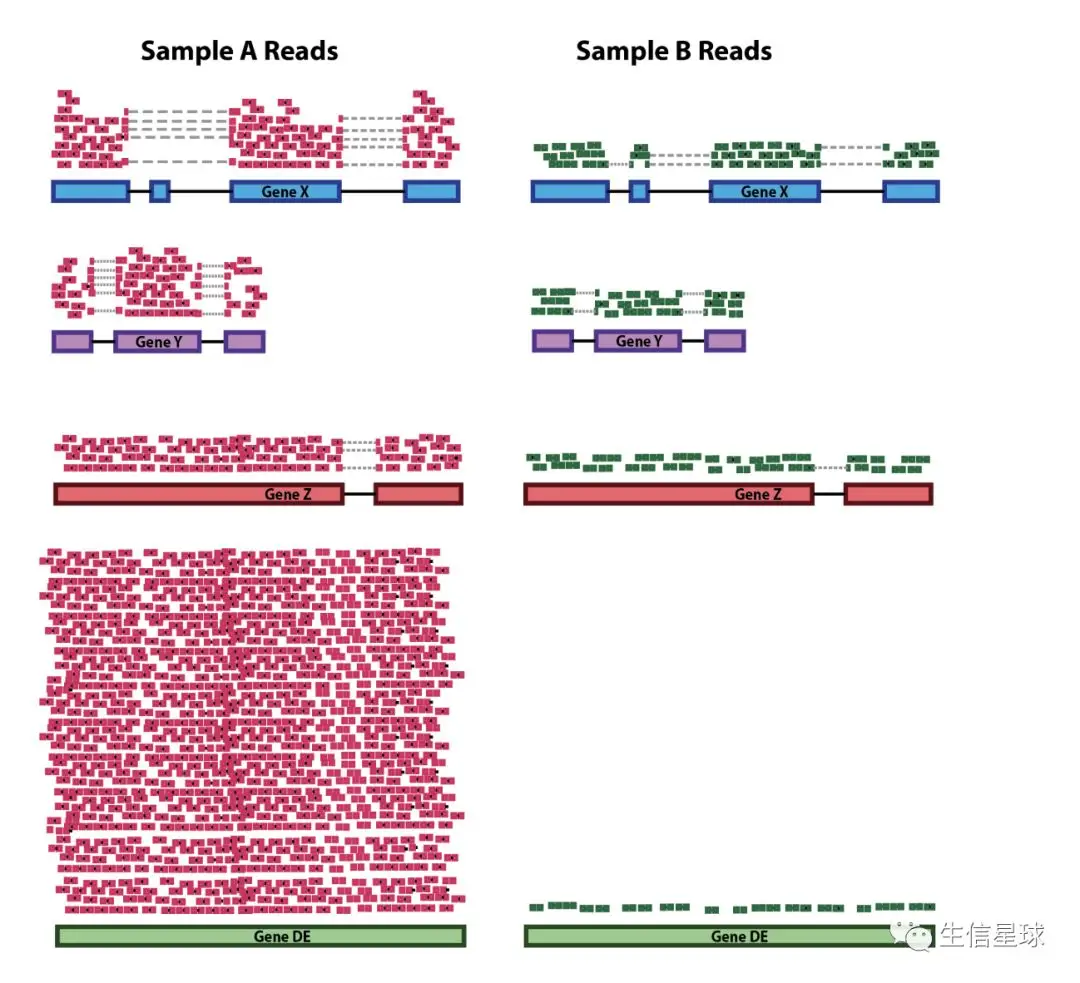
这种情况也可以理解为：找出搅局者。依然是在组间比较，但可能某个样本中就是存在这样的“异类”：它本身很强大，表达量超级高，拉高了整体的表达量，造成一种“虚假繁荣”。于是当按照前面的情况对测序深度做归一化处理时，“异类”的所有小伙伴都要陪着它一起缩小，为了减小所谓的“测序深度影响”。但它的小伙伴亏啊，本来和对照样本中的基因单挑是完胜的，但这一缩减，就不行了。就像下图中sample A的 gene DE，由于它的存在，sample A中其他基因的表达水平整体都要被拉低。

排除这一点可不太容易，因为这要求我们预先识别出这些“异类”基因，并且先把这些异类基因挑出去，剩下的才是用来做归一化的基因。不过现在已经有一些方法能够对其进行矫正了，下文中会详细介绍。

2024-06-17-144556.webp

归一化方法简介

CPM(counts per million)

CPM（每百万映射读数）是指将映射到转录本的原始读数数量，经过测序样本中的读数数量标准化后，乘以一百万。

具体来说，假设有n个基因（准确来说是基因的片段）映射到了参考基因组上，对于某个基因 $i$ ，其映射到参考基因组上的reads计数为 $x_i$ ，而全部基因在参考基因组上的reads计数和（map到所有基因的总reads数）为 $R=Σ(x_i)$ ，则CPM的计算公式是：

$$
CPM=\frac{x_i}{\sum x_i} \times 10^6
$$

由于 $R$ 是所有映射到参考基因组上基因计数的和，因此还有 $x_i/Σ(x_i)∈[0,1], Σ(x_i/Σ(x_i))=1$

举个例子，某次RNA-seq中测序了一个包含500万个reads读数的文库。其中，总共有400万个reads读数与基因组序列匹配，对于某个基因，有5000个计数在参考基因组上，则CPM为：

$$
(5000 \times 10^6)/(4 \times 10^6)=1250
$$

CPM对RNA-seq数据进行了测序深度的标准化，但没有考虑基因长度。因此，尽管它是一种样本内标准化方法，但CPM标准化不适用于对基因表达进行样本内比较。

RPKM与FPKM

  • RPKM=reads per kilobase of exon per million reads mapped
  • FPKM=fragments per kilobase of exon per million fragments mapped

FPKM 与 RPKM 非常相似。RPKM 是为单端 RNA-seq 制作的，其中每个读数对应一个已测序的片段。FPKM 是为配对末端 RNA-seq （双端测序）制作的。使用配对末端 RNA-seq，两个读数可以对应一个片段，或者，如果对中的一个读数没有映射，一个读数可以对应一个片段。RPKM 和 FPKM 之间的唯一区别是 FPKM 考虑到两个读取可以映射到一个片段（因此它不会将该片段计算两次）。

计算方法是，对于第 $i$ 个基因， $x_i$ 是map到这个基因的reads数， $N=Σ(x_i)$ 是总reads数， $l_i$ 是基因 $i$ 的长度。RPKM/FPKM的公式与CPM极为相似，除了分母多了 $l_i/10^3$ 这一项，用于矫正基因长度的影响。

$$
RPKM_i=\frac{x_i}{(l_i/10^3)(N/10^6)}
$$

RPKM/FPKM标准化方法只适用与样本内的比较，不适合用于样本间的比较。原因在于，对于不同的样本，总计数 $N=Σ(x_i)$ 是不相同的。举一个例子，样本1和样本2中的基因A的FPKM都是3.33，但是这两个样本的总计数 $N=Σ(x_i)$ 不一定相同，因此我们无法判断基因A在两个样本中的表达量是否相同。

TPM(transcripts per kilobase million)

CPM矫正了测序深度，适合相同基因在不同样本之间的比较；RPKM/FPKM矫正了基因长度，适合不同基因在同一个样本内的比较。有没有方法可以兼顾二者，既能样本内比较又能样本间比较呢？

当然有，这就是TPM方法，它既考虑测序深度，又考虑基因长度。对于TPM，其将分母部分的总计数 $N=Σ(x_i)$ 改为了使用基因长度标准化以后的总计数 $Σ_j(x_j/l_j)$ ，其计算方法可以等价为对RPKM的进一步标准化。

$$
TPM_i=\frac{x_i}{l_i}\times\frac{1}{\sum_j(x_j/l_j)}\times 10^6
$$

在使用TPM时，每个样本中所有TPM的总和是相同的，这样可以更轻松地比较每个样本中映射到基因的读数的比例。

可以这样认为：RPKM/FPKM方法首先考虑了测序深度，其次考虑了基因长度，而TPM先对基因长度进行标准化，然后对测序深度进行标准化。这种数学原理上的差异也导致上述归一化方法有不同的使用场景。

另外，我们可以按下述公式这么理解TPM：TPM相当于对RPKM的再一次矫正，弥补了RPKM跨样本比较时的不足之处。

$$
TPM_i \iff \frac{RPKM_i}{\sum_{j=1}^nRPKM_j}\times 10^6
$$

关于使用场景：

  • CPM适用于between-sample，不适用于within-sample
  • FPKM/RPKM适用于within-sample，不适用于between-sample
  • TPM都适用，但是由于没有对RNA composition做矫正，因此无法用于差异表达分析（DE analysis）

分位数矫正（quantiles normalization，QN）

分位数归一化是为了矫正RNA composition而出现的。简单来说，就是排序后求平均，然后再回序。

最初这种方法是为基因表达微阵列开发的（参考 https://www.nature.com/articles/s41598-020-72664-6 ），但现在几乎可以用于任何类型高通量测序数据的归一化分析，包括RNA测序和蛋白质组学。

下图展示了QN的步骤：

  • 首先在每个样本内对基因按表达量进行排序，并用排序的rank代替原先的表达量（表达量相同的基因用同一个rank；如下图的图1-2）；
  • 随后在样本之间计算每一个特定位序的rank的平均值（例如，各个样本在第二位序上基因表达量的rank分别是 [3,3,4,4,5,3,4,5] ，则计算平均值为 3.875，将其作为矫正之后的值（保留小数点后两位为3.88，如下图的图3）
  • 最后，将所有基因恢复为最初的排序，并且对于原先表达量相同（rank一致）但现在由于归一化而rank不一致的基因，再求一次均值（如下图的图4）

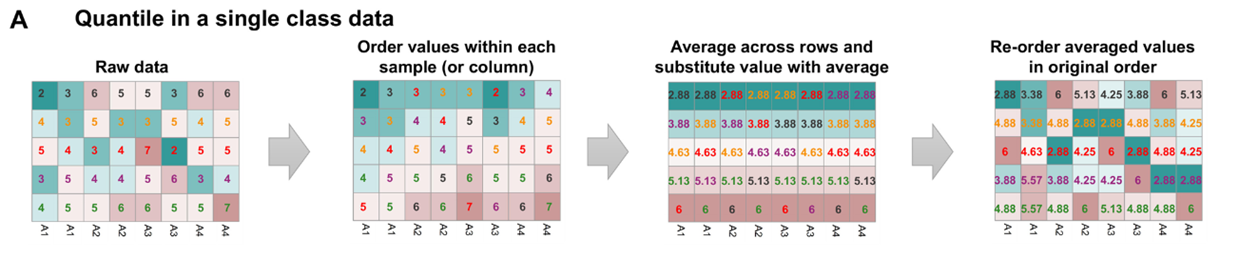
image.png

QN的原理简单易懂，且不需要提供基因长度等先验信息，因此在一些场景下很有用。然而，使用QN的一个特别危险是，外行分析师很容易被相当“完美”的归一化后结果误导：QN归一化样本看起来很相似，即使底层类别实际上非常不同。此外，QN可以在数据分析过程中消除真实信号并产生虚假信号。因此，在实际工作中，这种归一化方法应该谨慎使用。

在R包 preprocessCore 当中，已经提供了QN归一化的完整实现，因此如果需要QN归一化，直接调用上述R包即可。

DESeq2

DESeq2是一个很经典的差异表达分析工具包，最初发表于2014年，关于这个包的使用方法，网上的教程已经很丰富了，本文不再赘述。对于这个包的底层数学原理感兴趣的读者可以参考下面两篇参考文献

DESeq2采用一种叫做median of ratio的方法对raw count做归一化，步骤大致如下：

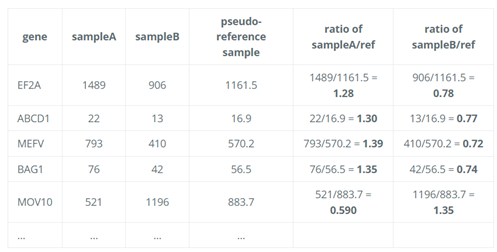
1. 创建伪参考样本（Pseudo-Reference Sample）

  • DESeq2 会为每个基因计算所有样本中表达量的几何平均值，形成一个“伪参考样本”。这个伪参考样本代表了所有样本中每个基因的“标准”表达水平。
  • 此处使用几何平均数而不是代数平均数，因为几何平均数对极端值不敏感，可以排除RNA composition的影响。
  • 计算方法：对于每个基因 $i$ ，计算所有样本中该基因计数的几何平均数

image.png

2. 计算每个样本与参考样本的比值

  • 对于每个样本 $j$ ，计算每个基因 $i$ 在该样本中的计数 $k_{ij}$ 与几何平均数（伪参考样本中该基因表达量）的比值。这些比值反映了每个样本相对于参考样本的表达水平变化。

image.png

3. 计算每个样本的归一化因子（Size Factor）

  • 根据上一步计算的比值，确定每个样本的归一化因子（也称为大小因子）。这个因子用来校正不同样本之间的测序深度差异。

  • 计算方法：对于每个样本 $j$ ，计算step2中比率的中位数，这个中位数就是size factor

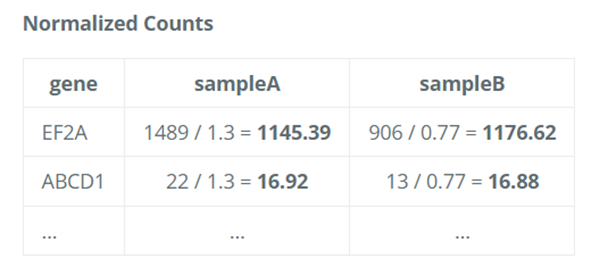
image.png

4. 使用归一化因子计算归一化后的计数值

  • 最后，使用计算出的归一化因子（大小因子）来调整每个样本的原始计数数据。
  • 具体来说，将每个样本的原始计数除以其对应的大小因子，得到归一化的计数值。

image.png

edgeR的TMM矫正

同DESeq2一样，edgeR也是一个著名的差异表达分析工具包，网上的使用教程非常丰富。想要了解算法细节的读者可以阅读下面的论文：

edgeR的归一化方法是trimmed mean of M values (TMM)方法。TMM 方法的核心思想是通过比较两个样本之间的整体表达水平来估计相对 RNA 产量。假设大多数基因不是差异表达的，可以通过这些基因的表达水平来估计相对 RNA 产量。

首先需要定义一下M值和A值。假设我们正在做样本k对样本r的差异表达分析，对于每一个基因 $g$ ，M值和A值定义如下：

$$
M_g=log_2\frac{Y_{gk}/N_{gk}}{Y_{gr}/N_{gr}}
$$

$$
A_g=\frac{1}{2}log_2((Y_{gk}/N_{gk})\times(Y_{gr}/N_{gr})), \text{ for } Y_{g·}\neq 0
$$

其中：

  • $Y_{gk}$ ：基因 $g$ 在样本 $k$ 中的raw count原始观察计数。
  • $N_k$ ：样本 $k$ 的总reads count次数。
  • $Y_{gr}$ ：基因 $g$ 在样本 $r$ 中的raw count原始观察计数。
  • $N_r$ ：样本 $r$ 的总reads count次数。

这两个值的生物学意义分别如下：

  • M值表示待比较组相对于参考组的表达水平变化程度（分母是实验组第g个基因的raw count在总count中占比，分子同理。M值就是实验组第g个基因相对于对照组的变化程度的对数值）。M值的正值表示待比较组的表达水平较高，负值表示待比较组的表达水平较低。
  • A值表示第g个基因在两组样本中的平均表达水平。

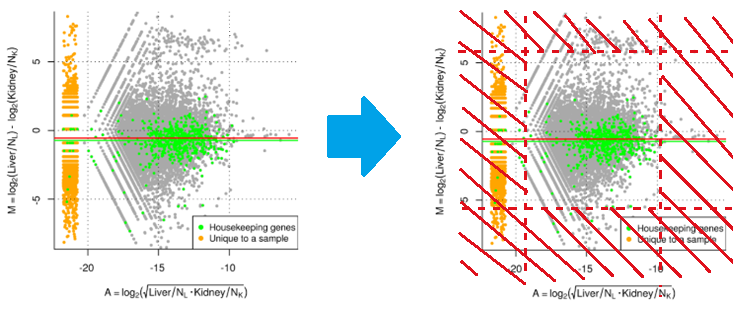
在TMM这个归一化方法中，我们主要用到的是M-value。例如，我们现在做样本k对样本r的差异表达分析，那么首先对样本k中的每一个基因g都算一下M-value，并根据edgeR方法推荐的阈值（M值修剪最大和最小的30%，A值修剪最大和最小的5%）对一些偏离较大的基因的M-value做截尾【也就是从M-value列表里删除这个基因的M-value】。剩下的M-value即为trimmed M-value，这些M-value对应的基因构成了集合 G* （如下图，我们对每个基因的M-value和A-value绘制散点图，如左图所示；trimmed M-value修剪步骤相当于右图中把外面这一圈的基因全都当作差异表达基因、给丢弃了，剩下中间那一圈基因被用来做后面的归一化处理）。

image.png

计算TMM回归系数还需要另外一个变量：基因权重 $w^r_{gk}$ 。这是raw count的逆方差。

$$
w^r_{gk}=\frac{N_k-Y_{gk}}{N_kY_{gk}}+\frac{N_r-Y_{gr}}{N_rY_{gr}}
$$

我们将集合 G* 中的M-value进行一个加权平均，得到的结果即为归一化因子TMM的对数（如下列公式所示）。将其进行log2的指数变换，即可得到样本k对样本r的归一化因子TMM。

$$
log_2(TMM^{(r)}_k)=\frac{\sum_{g\in G*}w^r_{gk}M^r_{gk}}{\sum_{g\in G*}w^r_{gk}}
$$

方法总结与对比

方法 基本原理 数学公式 优点 缺点 使用场景
CPM (Counts Per Million) 计算每个基因在特定样本中的计数值相对于总计数值的比例 CPM = Counts for gene / Total counts in library * 1,000,000 简单易懂，直观表示每个基因的相对丰度 受到样本间总计数差异的影响，不适用于比较不同样本的表达水平 用于快速评估样本间特定基因的相对表达水平
RPKM (Reads Per Kilobase per Million mapped reads) 计算每千碱基对每百万映射读数 RPKM = (Number of mapped reads for gene / Length of gene in kilobases) * (Total number of mapped reads in library / 1,000,000) 能够反映基因大小和表达量，适用于比较基因组大小不同的基因 需要对基因长度进行标准化，对基因长度分布不均的基因组不适用 用于基因组大小差异较大的物种或 基因组
FPKM (Fragments Per Kilobase per Million mapped fragments) 类似于RPKM，但基于片段而不是读数 FPKM = (Number of mapped fragments for gene / Length of gene in kilobases) * (Total number of mapped fragments in library / 1,000,000) 消除了基因大小的影响，更加准确地反映了基因表达量 同样需要对基因长度进行标准化，对基因长度分布不均的基因组不适用 与RPKM类似，适 用于基因组大小差异较大的物种或基因组
TPM (Transcripts Per Million) 计算每百万转录本的数量 TPM = (Number of mapped reads for gene / Total number of mapped reads in library) * (Length of gene in kilobases / Total length of all genes in kilobases) * (1,000,000) 通过转录本数量进行标准化，避免了基因大小的影响，更准确地反映基因表达量 需要转录本长度信息，对于不完全注释的基因组不适用 用于转录本数量较多的基因组，特别适用于多转录本基因的表达分析
TMM (Trimmed Mean of M-values) 通过去除极端值后计算的平均变异率进行标准化 不直接给出公式，而是基于M-values的计算，M-value = log2(Count) / Average count in sample 有效地减少了 极端值的影响，提高了数据的稳健性，适用于多种实验设计 对于小样本或数据分布不均匀的情况效果可能不佳 适用于需要标准化测序深度影响的各种RNA-seq实验设计，特别是当样本间存在显著的测序深度差异时