似然比检验(LRT):原理与应用
看论文的时候看到了这个方法,由于不懂就去学习了一下,顺带浅浅做了点笔记。
一、背景:似然值和最大似然法
“似然值”(likelihood)是统计学中用来衡量一种模型解释观测数据的好坏程度的一个指标。简单来说,似然值反映了在给定模型参数下,观测数据出现的概率有多大。
我们日常能够接触到的统计学一般是对样本或总体的探究,例如从一个大的总体中抽取有限数量的样本,从而估计总体的均值和方差,或者对两组样本进行统计检验,判断它们是否来自同一个总体。这些方法虽然也关注到了样本背后的总体,但对总体的概率分布模型参数并没有做过多的探究。
似然值则关注到了总体的概率分布模型。为了方便理解,我们可以画一个简单直观的图像,如下图所示。这是方差为1的正态分布(normal distribution)的概率密度曲线,其纵轴(概率值,probability)由样本值x和模型参数 $\mu$ (图中mu轴)共同决定。对于一个固定的参数mu,我们可以得到唯一的概率密度曲线,借助这个曲线我们可以进一步求出这一分布模型的期望值。例如,当mu=0时,对应的曲线就是均值为0、方差为1的标准正态分布曲线(图中红线),这一模型的期望值为0。
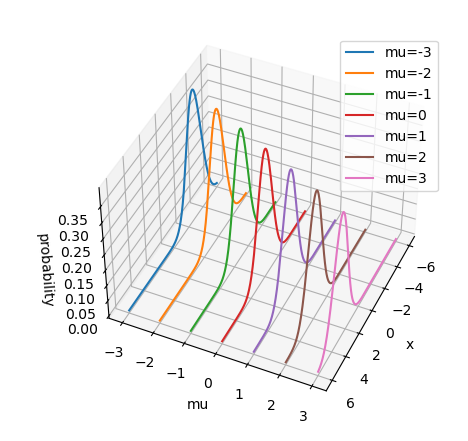
似然值则从另一个角度看待上述问题。它关心的是,当我们知道了一个概率分布模型的结论,如何反求这个模型的参数。例如,当我们已知一个正态分布模型的均值为1,要想求出这个模型的参数mu,可以在上图中x=1处做一个切面,研究各条曲线与这个切面的相交情况(如下图)。此时得到的曲线即为似然值曲线,横坐标为参数值,纵坐标为似然值(likelihood),似然值最大的点即为最有可能的参数值。
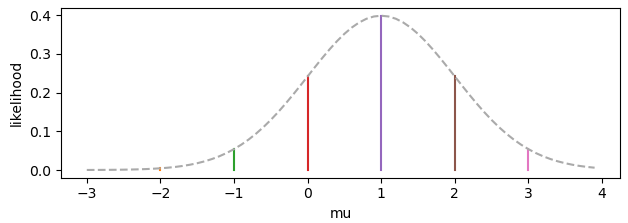
下面我们举一个实际点的例子。假设现在我们在探究抛掷一枚硬币出现正反面的概率,并且现在我们怀疑这枚硬币并非匀质,且正面朝上的概率为 $p$ (这里,“硬币并非匀质”就是对总体的概率分布模型的参数探究)。现在我们抛10次硬币,记录结果,结果发现有7次是正面朝上,3次是反面朝上。基于这样的观测结果,我们可以使用最大似然法对概率分布模型的参数 $p$ 进行探究:
- 模型设定:我们假定这枚硬币出现正面的概率是 $p$ ,反面的概率是 $1−p$ 。
- 似然函数:观测数据的概率可以表示为: $L(p)=P(7次正面, 3次反面∣p)=p^7×(1−p)^3$ 。
- 最大似然估计:最大似然法的原理就是找到上述似然函数的最大值,这个最大值就是最有可能的模型参数。
- 为了简化计算,我们一般会对似然函数取对数(由于对数函数是单调递增函数,因此似然函数和对数似然函数的极值点是相同的)。
- 上述似然函数的对数是 $\text{ln}L(p)=7\text{ln}p+3\text{ln}(1−p)$ ,求导得 $\frac{\text{d }\text{ln}L(p)}{\text{d}p}=7/p−3/(1−p)$ 。
- 令导数等于0,解方程得 $p=0.7$ ,这就是概率分布模型的参数 $p$ 的最大似然估计值。
通过最大似然估计,我们得到了 $p=0.7$ 。这意味着,在观测数据(10次中有7次正面)的情况下,最有可能的硬币正面朝上的概率是70%。
求解似然值的过程和求解概率值的过程可以看作两个相反的过程。求解概率值的过程是已知模型参数求事件发生次数(例如,已知不均匀硬币抛掷一次出现正面向上的概率为 $p=0.7$ ,求抛掷10次最有可能出现多少次正面向上的结果);而求解似然值则是已知结果求参数。
二、似然比检验要解决的问题
“似然比检验”(Likelihood Ratio Test, LRT)是一种统计检验方法,用来比较两个概率统计模型的好坏程度。
注意,此处用于比较的是两个概率统计模型(或者更实例化一点, 用于比较的是模型参数 ),而不是两个样本总体本身。
三、如何做似然比检验(LRT)
假设对于随机变量 $x$ ,其概率密度函数为 $f_\theta(x)$ ,其中模型参数 $\theta$ 未知。我们需要通过似然比检验确定 $\theta$ 的可能取值。
这里,我们需要提出两个假设用于检验:
- 原假设(H0):参数 $\theta$ 等于 $\theta_0$
- 备择假设(H1):参数 $\theta$ 不等于 $\theta_0$
似然比(likelihood ratio, $\Lambda$)是两个似然值的比值:
- $\Lambda = \frac{\text{在原假设 H0 下的最大似然值}}{\text{在备择假设 H1 下的最大似然值}}$
(注意,在一些教程中,似然比的定义是 $L(x)=\frac{sup{f_\theta(x):\theta\in \Theta_0}}{sup{f_\theta(x):\theta\in \Theta}}$ ,其中 $f_\theta(x)$ 指参数为 $\theta$ 的概率分布模型的概率密度函数,$\Theta_0$ 和 $\Theta$ 分别表示原假设和备择假设下的参数空间 ,$sup{}$ 是求上确界的意思。这种定义方式和上面的定义完全等价)
似然比如果等于1,说明原假设和备择假设没有区别。似然比越大,表明检验的结果越倾向于原假设H0;似然比越小,则越倾向于备择假设H1。
但是,仅凭似然比依然无法得到检验的结果。要决定是否拒绝原假设H0,还需要进行统计检验:
- 如果 $\Lambda>l$,则接受H0;
- 如果 $\Lambda\le l$ ,则拒绝H0接受H1。
这里的 $l$ 需要通过显著性水平 $\alpha$ 来确定: $\alpha=P(\Lambda \le l)$ ,其中 $P()$ 为概率测度(probability measure)。
但是,有时候很难通过这个关系式求出 $l$ 的具体值,因此可以使用 Wilks’ theorem 进行近似处理。
要介绍 Wilks’ theorem近似处理,首先我们需要定义一下对数似然比:
$$
\lambda_{LR}=-2\text{ln}\Lambda
$$
假设原假设为真,样本量 $n$ 近似无穷大,零假设的参数取值严格地位于参数空间的内部,那么上述统计量 $\lambda_{LR}$ 将近似服从一个卡方分布( $\chi^2$ ),且卡方分布的自由度等于两个模型参数个数的差。这就是 Wilks’ theorem近似处理的精髓,其允许我们使用卡方检验的方法进行似然比检验。
四、一个示例
仍然以上述抛硬币的实验为例。假设我们在研究这个硬币是否均一(即正面和反面的概率都是0.5),可以提出两个假设:
- 原假设(H0):硬币均一,正反面概率都是0.5。
- 备择假设(H1):硬币可能不均一,正反面概率不一定是0.5。
前面提到过似然值的计算方法是 $L(p)=P(7次正面, 3次反面∣p)=p^7×(1−p)^3$ 。按照原假设,最大似然值为 $L_0=0.5^7\times 0.5^3=1/1024\approx 0.00098$ ;按照备择假设,最大似然值为 $L_1=0.7^7\times 0.3^3\approx 0.00222$ (此处利用了前面的结论,既当 $p=0.7$ 时似然值最大)。
接下来我们需要计算似然比。在我们的示例中, $\Lambda=0.00098/0.00222\approx 0.44144$ ,虽然在一定程度上这表明模型倾向于备择假设H1,但我们需要做进一步的计算。
根据 Wilks’ theorem近似处理,检验统计量 $\lambda_{LR}=-2 \ln(\Lambda)\approx 1.63542$ ,自由度为1(因为H0是一个特例,只有一个参数 p = 0.5,而H1有一个自由参数 p)。
查找卡方分布表,自由度为1,显著性水平α = 0.05时,临界值为3.84。
由于 1.63542<3.84 ,检验统计量小于临界值,所以我们不能拒绝原假设。这意味着在显著性水平0.05下,没有足够的证据表明硬币是非均匀的。