连锁不平衡（Linkage Disequilibrium ）及其统计指标

发表于 更新于 分类于

在群体遗传学中，连锁不平衡是一个很重要的概念。前段时间看论文的时候看到了这个概念，于是专门花了点时间重温了一下相关知识点，顺带浅浅做了点笔记。

一、概念

连锁不平衡（Linkage Disequilibrium，LD ）是指一条染色体上的相邻位点之间的非随机关联，当一个位点上的某一等位基因与另一位点上的等位基因共同出现的概率大于随机组合的假设，则这两个位点之间存在连锁不平衡。

这个概念听起来有点抽象，下面结合一个实际例子进行解释。假设在同一条染色体上有A/a和B/b两个基因座位（由于它们在同一条染色体上，因此是连锁的）。在一个物种群体中，由于个体之间的随机交配以及同源染色体的交叉互换，理论上四种基因型AB,Ab,aB,ab都会出现，且基因型频率满足下面的关系：

$$
\begin{aligned}
p(AB)&=p(A)p(B) \\
p(Ab)&=p(A)p(b) \\
p(aB)&=p(a)p(B) \\
p(ab)&=p(a)p(b) \\
\end{aligned}
$$

其中 $p(AB),p(ab),p(aB),p(ab)$ 分别是四种基因型的频率， $p(A),p(a),p(B),p(b)$ 是四种等位基因的频率。

但许多时候，四种基因型频率并不满足上述的关系式，这种情况就是所谓的“连锁不平衡”。

一张图片用来解释连锁不平衡：

image.png

二、LD的常用统计量

首先我们定义一些符号，用下表中的这些符号分别表示基因型频率和等位基因频率。

基因型频率 A a 等位基因频率
B $\pi_{AB}$ $\pi_{aB}$ $\pi_{B}$
b $\pi_{Ab}$ $\pi_{ab}$ $\pi_{b}$
等位基因频率 $\pi_{A}$ $\pi_{a}$ $1$

（一）统计量D

$$
\begin{aligned}
D &= \pi_{AB}- \pi_{A} \pi_{B} \\
&= \pi_{ab}- \pi_{a} \pi_{b} \\
&= -(\pi_{Ab}- \pi_{A} \pi_{b}) \\
&= -(\pi_{aB}- \pi_{a} \pi_{B}) \\
&= \pi_{AB}\pi_{ab}-\pi_{Ab}\pi_{aB} \\
\end{aligned}
$$

统计量 $D$ 是许多LD统计量的基本组成部分，它某种连锁基因型的观测值（例如 $\pi_{AB}$ ）与期望值（例如 $\pi_{A}\pi_{B}$）之间的差异。请注意，上面虽然列出了5个式子，但它们之间都是等价的。

当连锁平衡时，观测值等于期望值，此时 $D=0$ 。连锁不平衡会使 $D$ 偏离0，但可能是往+1的方向偏离，也可能往-1的方向偏离。然而，由于 $D$ 的取值范围还会受到等位基因频率的影响，这不利于不同染色体片段之间的比较，因此很少有人单独使用 $D$ 统计量进行分析。

（二）标准化的D统计量：D’

$$
\begin{aligned}
D’ &= \left\{
\begin{aligned}
\frac{\pi_{AB} \pi_{ab} - \pi_{aB} \pi_{Ab}}{\min(\pi_{A}\pi_{b} \text{ , } \pi_{a}\pi_{b})} & \text{ , if } D > 0 \\
\frac{\pi_{AB} \pi_{ab} - \pi_{aB} \pi_{Ab}}{\min(\pi_{A}\pi_{B} \text{ , } \pi_{a}\pi_{b})} & \text{ , if } D < 0
\end{aligned}
\right. \\
&=\left\{
\begin{aligned}
\frac{D}{\min(\pi_{A}\pi_{b} \text{ , } \pi_{a}\pi_{b})} & \text{ , if } D > 0 \\
\frac{D}{\min(\pi_{A}\pi_{B} \text{ , } \pi_{a}\pi_{b})} & \text{ , if } D < 0
\end{aligned}
\right.
\end{aligned}
$$

$D’$ 统计量在 $D$ 统计量的基础上多加了一个分母用于标准化，并且根据 $D$ 的正负号的不同，这个分母的计算方式也有差异，从而保证了 $D’$ 是一个取值范围在 $[0,1]$ 之间的非负实数。

  • 当 $D’=0$ 时，四种基因型的频率完全符合预期，此时连锁平衡；
  • 当 $D’=1$ 时，只有至多三种基因型（单倍型）存在，两个位点之间的关系没有被重组打断，此时处于 完全的连锁不平衡状态（complete LD） 。
  • 除此之外的其他 $D’$ 取值都属于非完全的连锁不平衡状态。然而对于这些情况， $D’$ 统计量却无法获得更清楚的解释，因为样本量的大小会严重影响 $D’$ 的估值，导致样本之间不可比。

    （三） 另一种统计量： r2 和 Δ

$$
\begin{aligned}
r^2 &= \frac{D^2}{\pi_{A}\pi_{a}\pi_{B}\pi_{b}} \\
\Delta &= \frac{D}{\sqrt{\pi_{A}\pi_{a}\pi_{B}\pi_{b}}}
\end{aligned}
$$

$r^2$ 和 $\Delta$ 本质上是同一种统计量的不同叫法。和 $D’$ 不同， $r^2$ 使用了另一种方法对 $D$ 进行归一化。

$r^2=1$ 只有在一种非常严格的情况下成立，即两个位点上等位基因在染色体上的排列没有被重组打乱，而且等位基因具有完全相同的频率。此时的连锁不平衡状态被称为 完美的连锁不平衡（perfect LD） 。在这种情况下，样本中实际上只有两种单倍型（例如AB/ab或者Ab/aB），一个位点的信息完全可以替代另外一个位点，检测两个位点的基因型是多余的。

$r^2$ 的中间值比较容易解释，可以考虑两个位点，一个是与疾病关联的功能位点，另外一个是其附近的遗传标记位点，如果通过标记位点来检测与疾病之间的关联，想要达到与检测功能位点本身同样的功效的话，样本量需要增加大约 $1/r^2$ 倍。简单地讲，$r^2$ 的值与另外一个位点提供的信息含量是直接相关的。值得注意的是，这个性质已经很好地考虑了两个位点之间等位基因频率的差异。

然而，这也同样意味着两个紧密连锁、互相贴近的位点与第三个位点的连锁不平衡可能表现出完全不同的$r^2$ 值，所以小的$r^2$ 值并不意味着位点之间一定有高的重组率。另外一点，$r^2$ 受样本量大小的影响比 $D’$ 小得多。

从关联分析的功效角度对$r^2$ 的解释，产生了 实用连锁不平衡（useful LD） 的概念。在关联分析当中，由于病人样本，表型数据收集的困难以及基因分型的成本，样本量往往受到限制，况且花费很大的力气扩大样本量而使得标记与疾病易感位点之间的连锁不平衡微弱增加，实在是不可取。$r^2>\frac{1}{3}$ 的连锁不平衡水平，使得样本量的增加不超过3倍，可以作为“实用连锁不平衡”的底线。

（四）另外几种不算常用的统计量：δ、d、Q

$$
\delta=\frac{\pi_{AB}\pi_{ab}-\pi_{Ab}\pi_{aB}}{\pi_{B}\pi_{ab}}
$$

$$
d=\frac{\pi_{AB}}{\pi_{B}}-\frac{\pi_{Ab}}{\pi_{b}}
=\frac{\pi_{AB}\pi_{ab}-\pi_{Ab}\pi_{aB}}{\pi_{B}\pi_{b}}
$$

$$
\lambda=\frac{\pi_{AB}\pi_{ab}}{\pi_{Ab}\pi_{aB}}
$$

$$
Q=\frac{\lambda-1}{\lambda+1}
=\frac{\pi_{AB}\pi_{ab}-\pi_{Ab}\pi_{aB}}{\pi_{AB}\pi_{ab}+\pi_{Ab}\pi_{aB}}
$$

这几种统计量本质上也是对 $D$ 统计量的矫正或归一化。由于在文献中见到的较少，此处不做展开。

三、参考文献

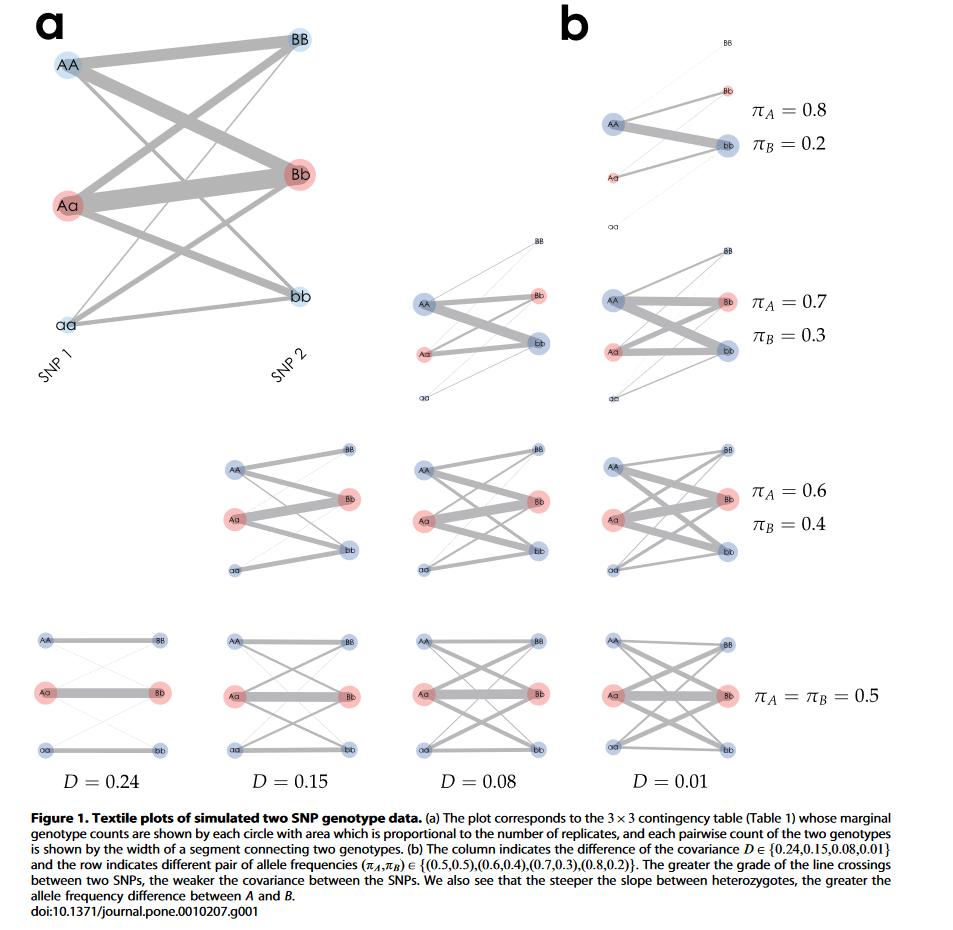
image.png

另外，有人开发过一个对染色体上LD区间进行可视化的工具（如上图），见TextilePlotpy - GitHub 。这个工具使用节点和线条来表示基因座之间的连锁关系，线条越粗表明连锁不平衡程度越高（例如上图展示的例子从左到右的D值在减小，即连锁不平衡程度在降低）。但是，由于长时间缺乏维护，这个工具目前无法直接运行，需要对代码进行一定的修改调整，限于篇幅本文没有进行进一步的探究。

以上。