机器学习可解释性实操

发表于 2024-04-22 分类于计算机

本文简单介绍了可解释机器学习的研究背景，并结合python的sklearn接口简单探索了一些实现事后机器学习可解释性的方法。这些方法将对实际应用中的数学模型搭建和分析起到重要的作用。

一、背景与必要的知识

（一）机器学习可解释性的提出背景

近些年来，以深度学习为主的方法在AI的各个领域内都取得了丰硕的成绩。基本上人能做或者不能做的事情，大家都想用AI解决。然而相比于线性回归、决策树等传统的建模方法，深度学习方法的缺点在于其内部结构相当于一个“黑盒”，我们并不知道模型的每个决策是如何做出的。

另一方面，即使是传统的模型，如果能使用一些方法进行更深层次的profile，则也会有着非常重要的意义，例如可以基于此了解特征之间的互作关系。

为了解决模型的“黑盒”问题，科学家们提出了可解释机器学习。除了预测的精准性之外，可解释性也是机器学习模型是否值得信赖的重要衡量标准。

解释指的是用通俗易懂的语言进行分析阐明或呈现。对于模型来说，可解释性指的是模型能用通俗易懂的语言进行表达，是一种能被人类理解的能力，具体地说就是，能够将模型的预测过程转化成具备逻辑关系的规则的能力。

可解释性通常比较主观，对于不同的人，解释的程度也不一样，很难用统一的指标进行度量。我们的目标是希望机器学习模型能“像人类一样表达，像人类一样思考”，如果模型的解释符合我们的认知和思维方式，能够清晰地表达模型从输入到输出的预测过程，那么我们就会认为模型的可解释性是好的。

（二）可解释性的分类

根据不同的使用场景，我们大致可以将模型的可解释性作以下分类。

1. 内在可解释VS.事后可解释

内在可解释（Intrinsic Interpretability） 指的是模型自身结构比较简单，使用者可以清晰地看到模型的内部结构，模型的结果带有解释的效果，模型在设计的时候就已经具备了可解释性。
事后可解释（Post-hoc Interpretability） 指的是模型训练完之后，使用一定的方法增强模型的可解释性，挖掘模型学习到的信息。

2. 局部解释VS.全局解释

对于模型使用者来说，不同场景对解释的需求也有所不同。对于整个数据集而言，我们需要了解整体的预测情况；对于个体而言，我们需要了解特定个体中预测的差异情况。

局部解释 指的是当一个样本或一组样本的输入值发生变化时，解释其预测结果会发生怎样的变化。
全局解释 指的是整个模型从输入到输出之间的解释，从全局解释中，我们可以得到普遍规律或统计推断，理解每个特征对模型的影响。

（三）研究方向概览

目前机器学习领域已经提出的模型中，如果按模型可解释性和模型精度来划分，则会呈现出下图这种场景。诸如线性回归、决策树等传统模型固然内在可解释性很好，但在面对复杂问题时的精度较低；而神经网络、支持向量机等方法的预测精度很好，但内在可解释性不足。似乎没有模型能够同时满足“预测精度好”和“可解释性好”这两个指标。

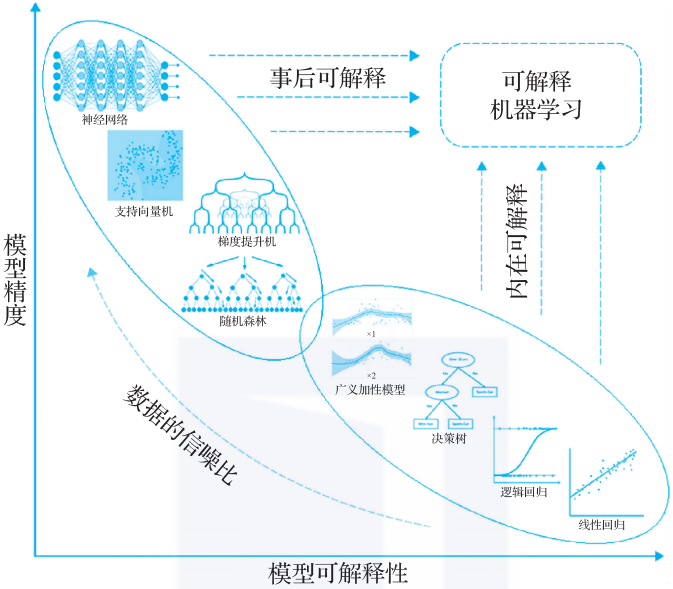
因此，针对模型评价的两个指标，可解释机器学习有两大研究方向，具体说明如下。

第一，对于传统的统计学模型（比如决策树、逻辑回归、线性回归等），模型的可解释性较强，我们在使用模型时可以清楚地看到模型的内部结构，结果具有很高的可解释性。
- 然而一般情况下，这些模型的精度较低，在一些信噪比较高（信号强烈，噪声较少）的领域，拟合效果没有当下的机器学习模型高。
- 在保持模型的可解释性前提下，我们可以适当地改良模型的结构，通过增加模型的灵活表征能力，提高其精度，使得模型往纵轴正方向移动，形成内在可解释机器学习模型。
- 比如，保持模型的加性性质，同时从线性拟合拓展到非线性拟合，GAMI-Net、EBM模型均属于内在可解释机器学习模型。
第二，当下的机器学习模型（比如神经网络、深度学习），其内部结构十分复杂，我们难以通过逐层神经网络或逐个神经元观察数据的变化，在一些信噪比较低（信号较弱，噪声强）的领域，我们很容易把噪声也拟合进去，不易发现其中的错误，模型的可解释性较低。
- 为了提高模型的可解释性，我们可以采用以下两种方法：
  - 降低模型结构的复杂度，如减少树模型的深度，以牺牲模型的精度换取可解释性；
  - 保持模型原有的精度，在模型训练完之后，利用事后辅助的归因解析方法及可视化工具，来获得模型的可解释性。
- 无论采用哪一种方法，其目的都是让模型往横轴的正方向移动，获取更多的可解释性。

本文主要是对机器学习可解释性方法的简要介绍，此外我们将利用sklearn提供的函数接口和示例数据集，介绍几种较为经典的事后可解释性方法（部份依赖图、个体条件期望图、置换特征重要性检验）。这些方法非常简单实用，但可以满足大多数模型的事后可解释性的研究。

二、部份依赖图（Partial dependence plots，PDP）

“部分依赖图”（Partial Dependence Plot，PDP）是机器学习模型解释和可解释性分析的一种工具，它主要用于可视化单个特征（或输入变量）对模型预测结果的影响（与此同时，边缘化所有其他输入特征的值）。在机器学习中，模型往往包含多个输入变量（也称为特征），这些变量之间可能存在复杂的相互作用。 PDP通过展示每个特征值的变化如何单独影响模型输出，从而帮助我们理解模型的行为。直观地，我们可以将部分依赖性解释为作为感兴趣的输入特征的函数的预期目标响应。

在此，我们定义“感兴趣的输入特征”（input features of interest）是要用可解释机器学习方法进行分析的所有特征，而“补充特征”（complement features）是剩余的所有被模型所包含、但我们并不关心或不去分析的特征。

PDP的工作原理如下：

固定其他特征：对于一个给定的预测目标，PDP会固定所有其他输入特征在训练数据的平均值或某个特定值，只改变目标特征的取值范围。
计算预测：对于每一个特征值，模型会计算出相应的预测结果。
绘制曲线：将特征值与对应的预测结果绘制成一条线或者一个区域图，形成部分依赖图。如果预测值随着特征值增加而增加，那么曲线通常是上升的；如果预测值与特征值无关或负相关，曲线则基本平坦或下降。

通过观察PDP，我们可以直观地了解：

某个特征对模型预测的重要性：特征值变化较大时，对应曲线变化明显，说明该特征对预测有较大影响。
特征之间的交互：如果一个特征的PDP曲线在另一个特征的值变化时有所改变，可能表明这两个特征存在交互效应。
预测的稳定性和敏感性：如果曲线平滑且变化较小，说明模型对该特征的预测相对稳定；反之，如果曲线波动大，可能表示模型对该特征的预测较为敏感。

部分依赖图是黑盒模型（如随机森林、神经网络等）可解释性分析的重要工具，它可以帮助我们理解模型决策的基础，从而增强模型的透明度。

下图显示了使用HistGradientBoostingRegressor在共享单车数据集上建立的模型中，温度和湿度这两个因素的部分依赖图（图片来自sklearn官方教程）：

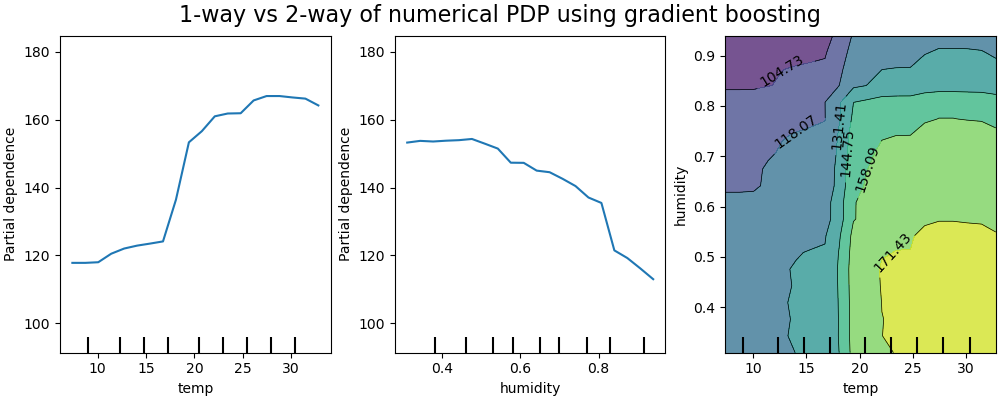
PDP-sklearnofficial

单路PDP（1-way PDP）告诉我们目标响应和单个输入特征之间的相互作用。上图中的左图显示了温度对自行车租赁数量的影响；我们可以清楚地看到，更高的温度与更高的自行车租赁数量有关。同样，我们可以分析湿度对自行车租赁数量的影响（中间图）。因此，如果一次只考虑一个特征，这些解释是边缘的。
双路PDP（2-way PDP）则可以显示两个特征之间的相互作用。例如，上图中的右图显示了自行车租赁数量对温度和湿度联合值的依赖性。我们可以清楚地看到这两个特征之间的相互作用：温度高于20摄氏度，主要是湿度对自行车租赁数量有很大影响。对于较低的温度，温度和湿度都会影响自行车租赁的数量。

sklearn.inspection模块提供了一个函数from_estimator，用于创建1-way和2-way PDP。

下面是一个实际的例子，我们在糖尿病疾病进展数据集上使用支持向量机回归（SVR）方法构建了一个回归模型，然后使用PDP对模型进行解释。这一数据集收集了BMI、BP（血压）、sex（性别）、age（年龄）、s1（total serum cholesterol，总血清胆固醇）、S2（低密度脂蛋白）、S3（高密度脂蛋白）等因素对糖尿病患者疾病进展情况（disease progression）的影响，除了sex这一特征以外，其余特征均为连续变量。

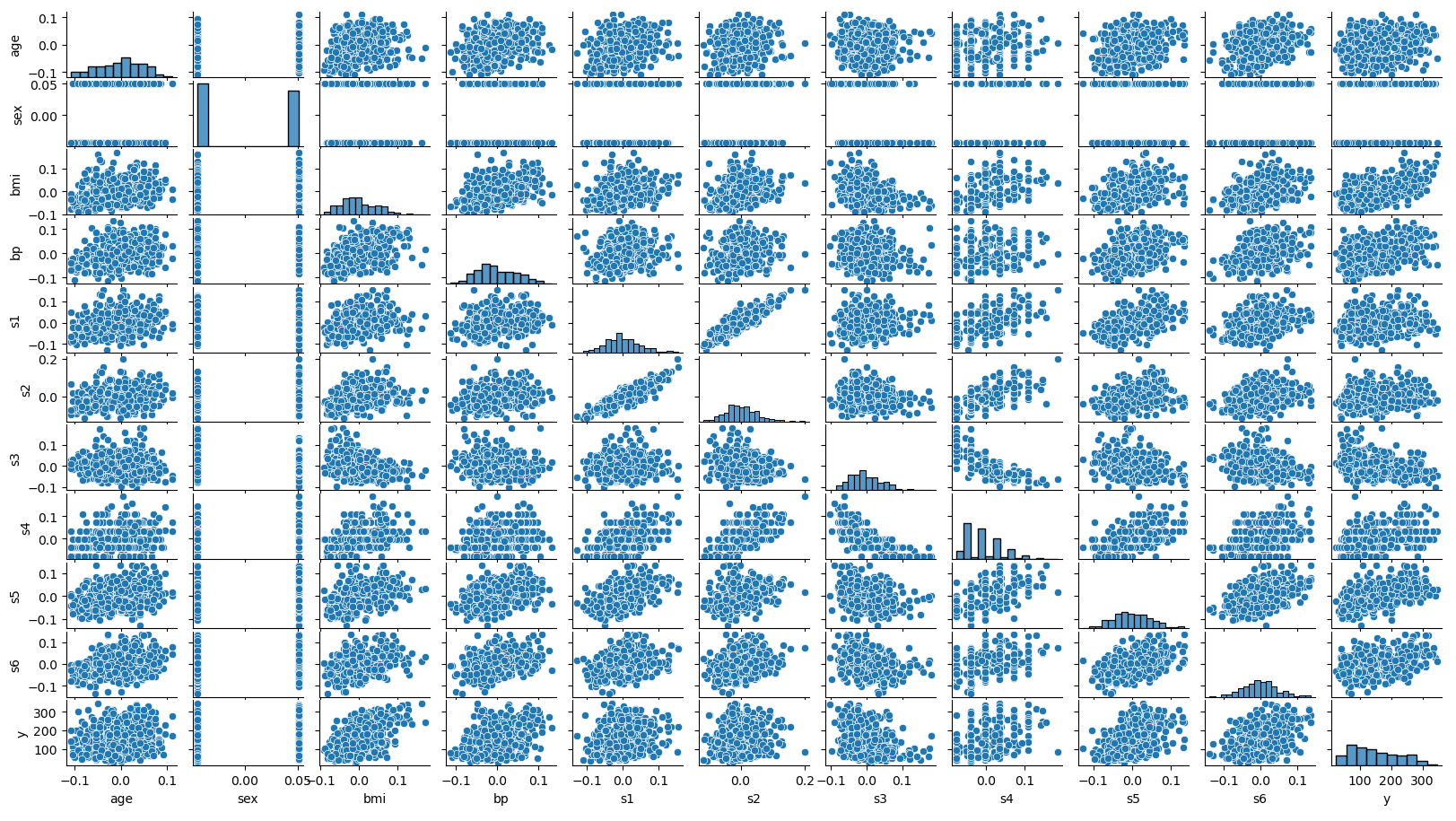
首先我们导入数据集，使用pairplot看一下数据分布情况，并建立SVR回归模型，代码如下：

from sklearn.datasets import load_diabetes # 数据集的导入函数
from sklearn.svm import SVR # 支持向量机回归方法
import pandas as pd
import numpy  as np
# 加载数据集
diabetes_data = load_diabetes() 
X = pd.DataFrame(diabetes_data["data"])    # 获取自变量X
X.columns = diabetes_data["feature_names"] # 设置自变量X的特征名称
y = diabetes_data["target"] # 获取数据集中的响应变量y
# 下面几行代码用来画一个pairplot图，看一看数据分布情况
dataset_to_display = X.copy()
dataset_to_display["y"] = y
import seaborn as sns
sns.pairplot(dataset_to_display)
# 建立数学模型。SVR方法建模，超参数全部用默认参数
reg = SVR().fit(X, y)

接下来，我们使用1-way PDP看一下这些自变量对响应变量的影响：

from sklearn.inspection import PartialDependenceDisplay # PDP模型解释函数
import matplotlib.pyplot as plt
features_interest_1way = np.arange(X.shape[1])
PartialDependenceDisplay.from_estimator(reg, X, # 要解释的模型和自变量
    features=features_interest_1way, # 这个参数是要解释的自变量的下标
    grid_resolution=10) # 网格搜索分辨率，分辨率越高PDP越精确，但速度也越慢。默认100，如果想要快一点出图可以调得更小
plt.show()

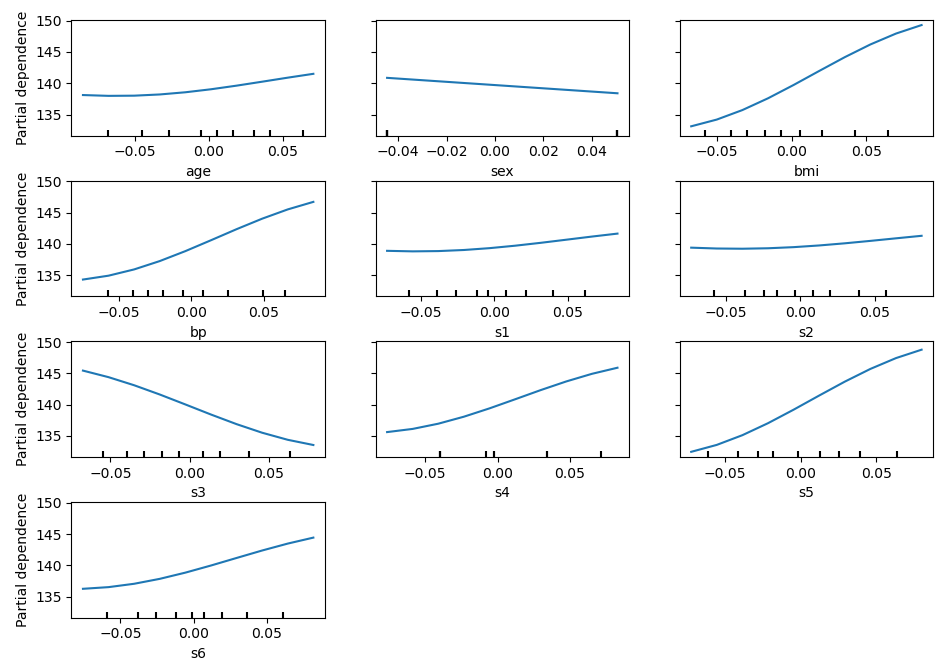
从图上看，似乎BMI、BP（血压）、S3（总胆固醇/HDL）、S5（血清甘油三酯水平可能对数）这几个特征对响应变量贡献比较大（曲线有更大的起伏）。

下面，我们再来看看2-way PDP，看看这些特征之间的相互作用。由于特征数量较多，我们只挑选部分特征进行2-way PDP的绘制

from sklearn.inspection import PartialDependenceDisplay # PDP模型解释函数
import matplotlib.pyplot as plt
interest_feature_index = [2,3,6,7,8] # 挑选的特征下标
features_interest_2way = []
for i in range(5):
    for j in range(i+1,5):
        features_interest_2way.append((interest_feature_index[i],
            interest_feature_index[j]))
PartialDependenceDisplay.from_estimator(reg, X, 
    features=features_interest_2way, # 这个参数是要解释的自变量的下标，注意2-way PDP传入的是一组元组，每个元组中包括两个特征的下标
    grid_resolution=10)
plt.show()

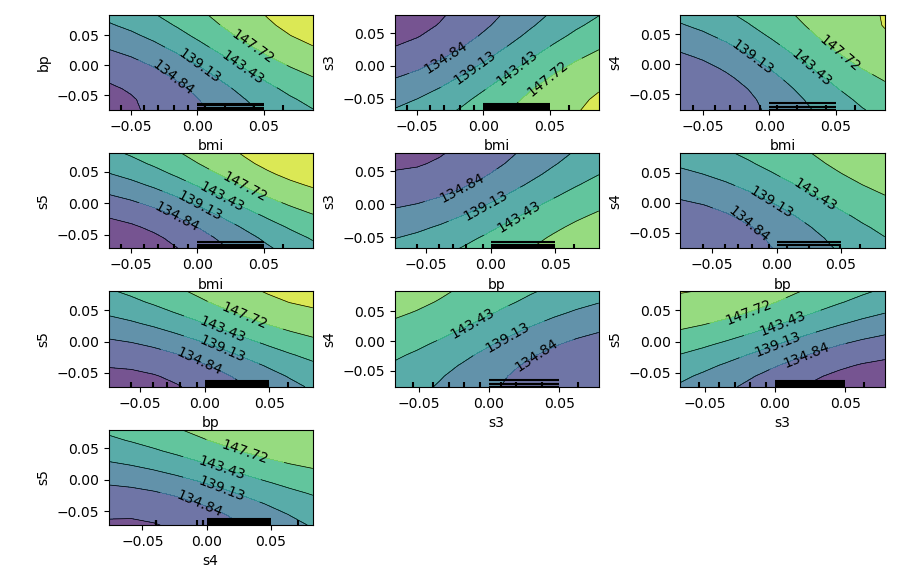
从图中可以看出，对糖尿病疾病进展有重要作用的特征包括BMI、BP、S1等等，并且可以看出它们之间的相互作用。

三、个体条件期望图（Individual conditional expectation plot，ICE）

与PDP类似，个体条件期望图（ICE）显示了目标函数和感兴趣的输入特征之间的相关性。然而，与显示输入特征的平均效果的PDP不同，ICE图对每个样本预测结果各自的特征依赖性进行了可视化，每个样本分别绘制一条线。一副ICE图只支持可视化一个感兴趣的输入特征。

仍以共享单车数据集为例，下图显示了使用HistGradientBoostingRegressor建立的模型中，温度和湿度这两个因素的ICE图（图片来自sklearn官方教程）：

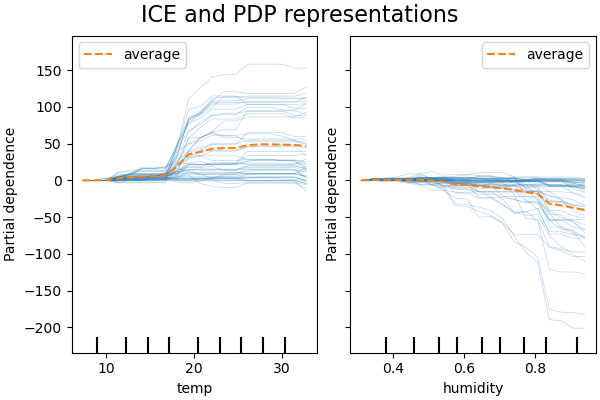
图中的每一条蓝色细线代表一个样本在预测过程中的特征依赖性。虽然PDP善于显示目标特征的平均效果，但它们可能会掩盖由交互创建的异构关系。当特征间的互作出现时，ICE图将提供更多的见解。例如，我们看到温度特征的ICE提供了一些额外的信息：一些ICE线是平的，而另一些则显示出对35摄氏度以上温度的依赖性降低。我们观察到湿度特征的类似模式：当湿度超过80%时，一些ICE线显示出急剧下降。

sklearn.inspection模块的PartialDependenceDisplay.from_estimator函数不仅可以用于创建PDP图，还可以用于创建ICE图，只需要设置参数kind='individual'即可。设置参数centered=True可以对ICE图进行中心化处理，从而方便对结果的查看。

下面我们仍以糖尿病数据集为例进行实操：

from sklearn.datasets import load_diabetes
from sklearn.svm import SVR
from sklearn.inspection import PartialDependenceDisplay
import pandas as pd
import numpy  as np
import matplotlib.pyplot as plt
diabetes_data = load_diabetes() # 加载数据集
X = pd.DataFrame(diabetes_data["data"][:,0:5])  # 获取数据集中的自变量X，并保留前四列
X.columns = diabetes_data["feature_names"][0:5] # 获取数据集中的自变量X的特征名称
y = diabetes_data["target"] # 获取数据集中的响应变量y
reg = SVR().fit(X, y)
features_interest_1way = np.arange(X.shape[1])
PartialDependenceDisplay.from_estimator(reg, X, 
    features=features_interest_1way,
    kind='both',   # 同时绘制PDP图和ICE图，以便观察。
    centered=True, # 按x轴第一个点的数值进行中心化处理。
    grid_resolution=10)
plt.show()

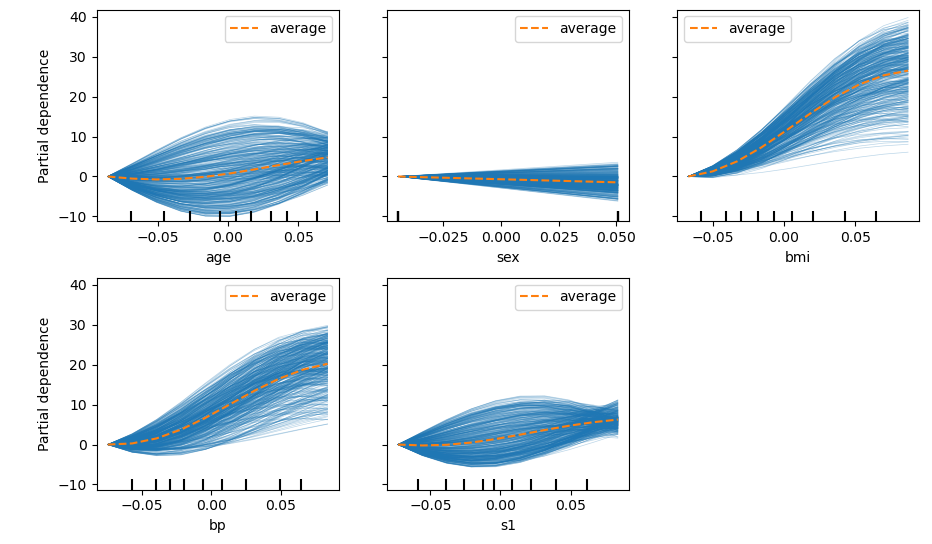
PDP图可以看作ICE图所有曲线的平均。如上图所示，我们可以看到包括BMI、BP、S1等在内的诸多因素都对糖尿病进展有重要性，虽然如此S1性状（血清胆固醇）的ICE提供了一些额外的信息：一些ICE线随S1的变化先增高后降低，另一些则与之相反，先降低后增高。

四、置换特征重要性（Permutation feature importance）检验

置换特征重要性是一种模型检查技术，用于测量每个特征对给定数据集上拟合模型统计性能的贡献。这种技术对黑箱模型特别有用，它的原理大体上涉及随机打乱单个特征的值，并观察模型得分的下降。通过打破特征和目标之间的关系，我们可以确定模型在多大程度上依赖于这种特定特征。

在下图中，我们观察到置换特征对特征和目标之间的相关性的影响，以及对模型统计性能的影响（图片来自sklearn官方教程）：

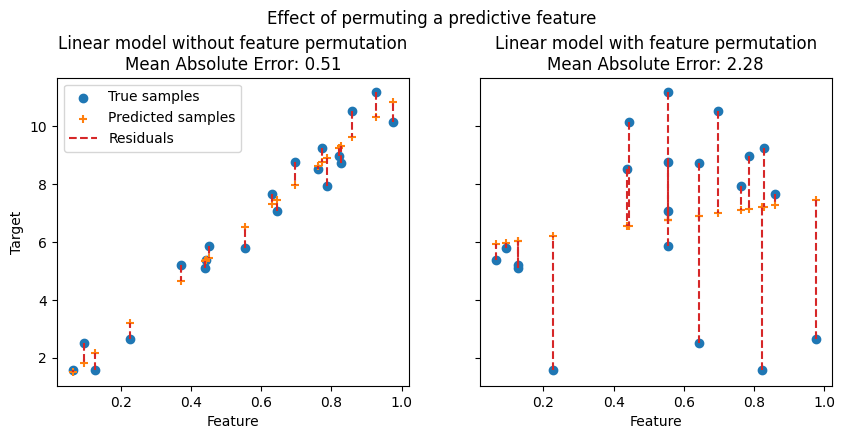
每幅图的横坐标都是特征的取值，纵坐标是相应目标（ $Y$ ）的取值。左侧的图是置换之前的图，右侧的图是置换之后的图。对于预测性的特征（上面两图），对特征进行置换会破坏特征和目标之间的相关性，从而降低模型的统计性能（Mean Absolute Error显著增高）。对于非预测性的特征（下面两图），对特征进行置换并不会显著降低模型的统计性能。

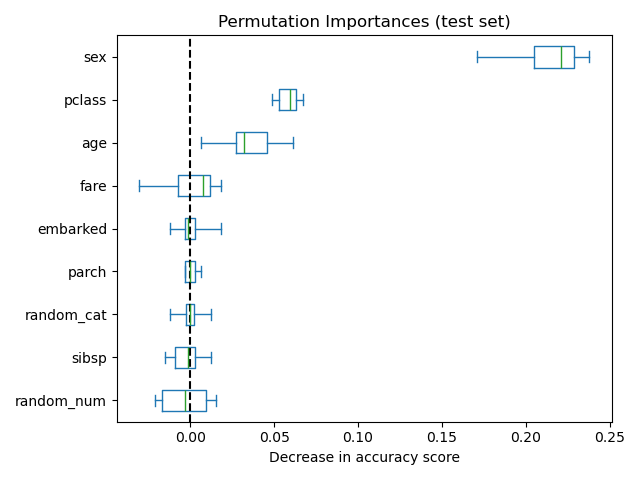
置换特征重要性的一个关键优点是它是“模型不可知的”（model-agnostic），即它可以应用于任何拟合的估计器。此外，它可以多次进行特征置换的计算，从而为特征重要性的估计提供了方差度量（多次置换并计算统计性能的降低，然后可以对这种统计性能上的降低进行方差的计算）。如下图是使用随机森林方法对泰坦尼克幸存人员数据集的建模结果（其中人为的加入了两个随机数特征random_cat和random_num，它们仅为随机取值，不包含任何信息），使用特征重要性检验可以看出性别、乘客等级、年龄等特征都很重要，而正如我们预期的那样，两个随机数特征random_cat和random_num的置换特征重要性近乎为零。（图片来自sklearn官方教程）

下面我们再以糖尿病数据集为例进行实操。首先我们继续使用支持向量回归（SVR）建模：

from sklearn.datasets import load_diabetes
from sklearn.svm import SVR
import pandas as pd
import numpy  as np
import matplotlib.pyplot as plt
diabetes_data = load_diabetes() # 加载数据集
X = pd.DataFrame(diabetes_data["data"])    # 获取数据集中的自变量X
X.columns = diabetes_data["feature_names"] # 获取数据集中的自变量X的特征名称
y = diabetes_data["target"] # 获取数据集中的响应变量y
reg = SVR().fit(X, y)
reg.score(X,y) # 输出0.2071777370990262

下面使用sklearn提供的方法permutation_importance进行置换特征重要性检验。需要的传入参数包括模型、数据集以及置换检验次数，也可通过scoring参数指定不同的模型评价指标。

from sklearn.inspection import permutation_importance
r = permutation_importance(reg, X, y,
                           n_repeats=30,
                           random_state=0,
                           scoring="r2")
for i in r.importances_mean.argsort()[::-1]:
    if r.importances_mean[i] - 2 * r.importances_std[i] > 0:
        print(f"{X.columns[i]:<8}"
              f"{r.importances_mean[i]:.3f}"
              f" +/- {r.importances_std[i]:.3f}")

输出：

bmi     0.058 +/- 0.005
s5      0.056 +/- 0.006
bp      0.035 +/- 0.004
s3      0.030 +/- 0.004
s4      0.026 +/- 0.004
s6      0.015 +/- 0.003
age     0.011 +/- 0.002
s1      0.010 +/- 0.002
s2      0.009 +/- 0.002
sex     0.006 +/- 0.002

还可以对这些结果进行可视化展示：

# 利用pandas的dataframe对置换特征重要性检测结果进行一些预处理和排序
import pandas as pd
rdf = pd.DataFrame(r.importances)
rdf.index = X.columns
rdf["mean"] = r.importances_mean
rdf = rdf.sort_values(by="mean",ascending=False)
rdf = rdf.T
rdf = rdf.drop("mean",axis=0)
# 之后，使用seaborn进行数据可视化
import seaborn as sns
sns.boxplot(rdf,orient="h")
plt.plot([0,0],[-1,rdf.shape[1]],color="#222",linestyle="--")
plt.xlabel("Decrease in accuracy score")
plt.title("permutation importances")
plt.show()

结果如下图所示：

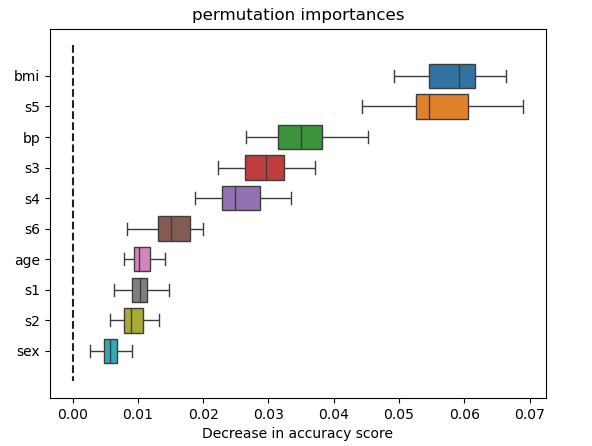
需要注意的一点是，对于坏模型来说重要性较低的特征（低交叉验证分数）对于好模型来说可能非常重要。因此，在计算特征重要性之前，使用交叉验证等方法评估模型的预测能力总是很重要的。置换重要性并不反映特征本身的内在预测值，而是反映该特征 对特定模型的 重要性。

五、参考文献与拓展阅读

参考：

拓展阅读：

课本： Explainable Artificial Intelligence：An Introduction to Interpretable Machine Learning
R包&python模块： DALEX 。相关资源： Github 。这一模块有其官方课本。下图为DALEX的文档中对机器学习可解释性的分层。

关于机器学习可解释性，在事后解释（post-hoc）方面，主要的方法包括PDP图、ICE图等，这一部分内容详见下面这些参考资料

偏回归图与偏残差图 - vacleon的文章 - 知乎

Partial Dependence Plots —— 部分依赖图 - 冰焰虫子的文章 - 知乎

机器学习模型可解释性进行到底 ——PDP&ICE图（三） - 悟乙己的文章 - 知乎

机器学习模型可解释性进行到底——特征重要性（四） - 悟乙己的文章 - 知乎

chapter 3.7 Traditional Interpretable Algorithms. in book: “Explainable Artificial Intelligence：An Introduction to Interpretable Machine Learning”, p102.

R语言可解释性机器学习（五）部分依赖图（PDP） - 修身立道的文章 - 知乎

在DALEX的网站中，提供了一些视频研讨会的录像，例如 useR! 2020: Keynote + Farewell - Talk with your model!