Attention机制与self-attention详解（一）——基础知识

发表于 更新于 分类于

时隔半年，再次复习一下attention机制，并学习一下什么是self-attention。

参考： https://www.bilibili.com/video/BV1v3411r78R

一、attention机制

（一）attention要解决的问题

  • 当输入是一个可变长度的sequence时（就是说，输入一组向量vector，但是向量总数不确定），传统的神经网络适应能力不佳
    • 可变长度的输入示例：文本序列、音频序列、图片
      • 对于文本序列输入，需要一步预处理，将文本中的每个单词用向量进行编码
        • 一种表示方法是one-hot encoding，但会导致向量维度太高，并且无法反映词汇之间的关系
        • 另一种方法是word embedding
      • 音频序列一般会按帧长度将序列分割成一段一段的帧，每一帧转化为一个向量
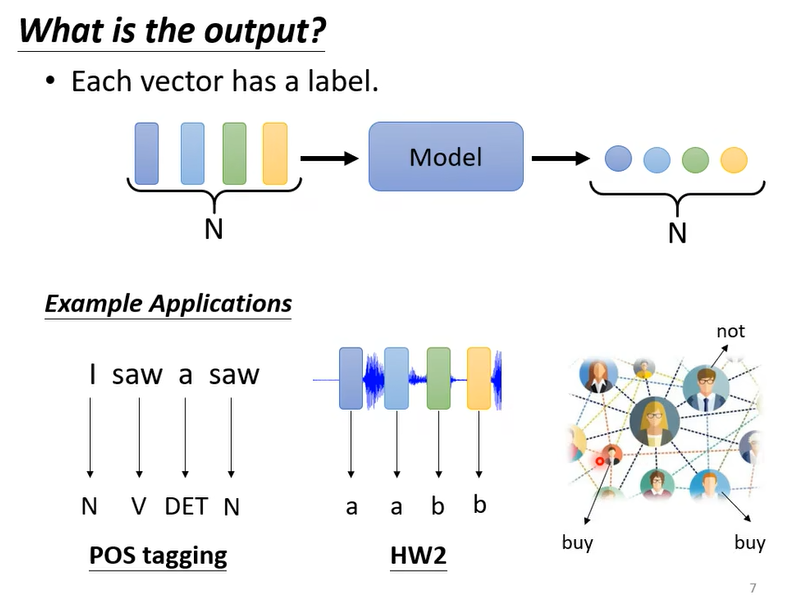
  • 输出任务：
    • 1、each vector has a label，每个向量预测一个标签。例如词性标注（每个单词都输出一个词性的标签）、语音识别
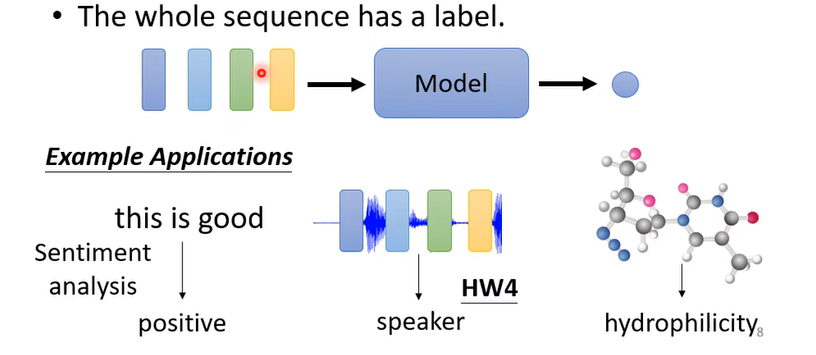
      • image.png
    • 2、the whole sequence has one label，整条序列预测一个标签。例如文本情感标注，输入一段话（由若干单词组成），输出一个情感类别的符号。
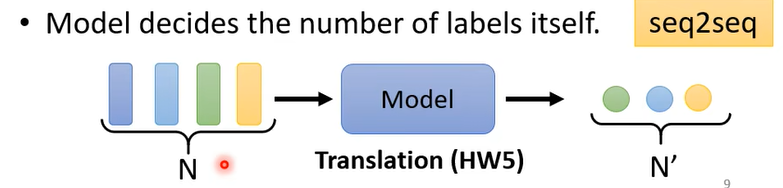
      • image.png
    • 3、输出的标签个数由模型自己决定，即seq2seq任务，例如翻译任务（输入的向量数量和输出的标签数量并不存在一对一的关系）
      • image.png

（二）self-attention的结构

  • sequence labeling问题（上述输出任务1）
    • 一种方法是用fully-connected network（FC network），即全连接神经网络
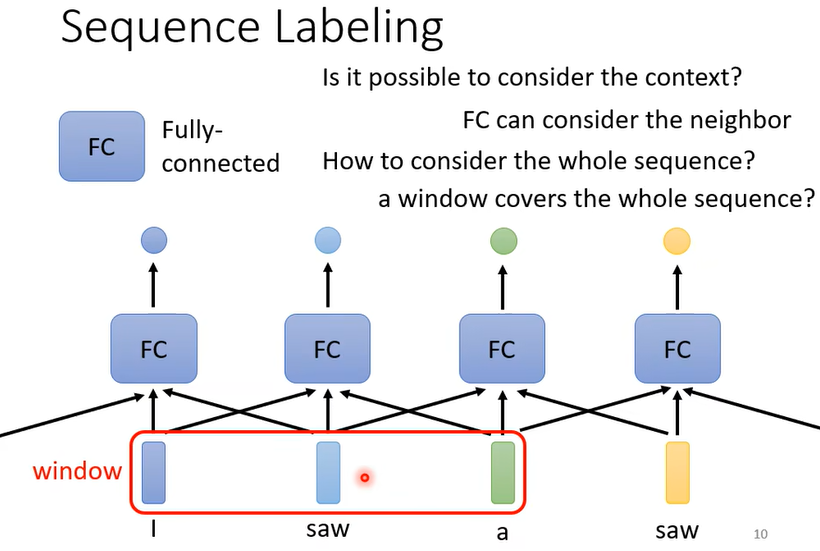
    • image.png
    • 但是输入的文本是可变长度的，如果FC network要想考虑全部的输入，需要开一个很大的window，但这会导致模型过于庞大
    • 另一种解决方法是使用self-attention的结构
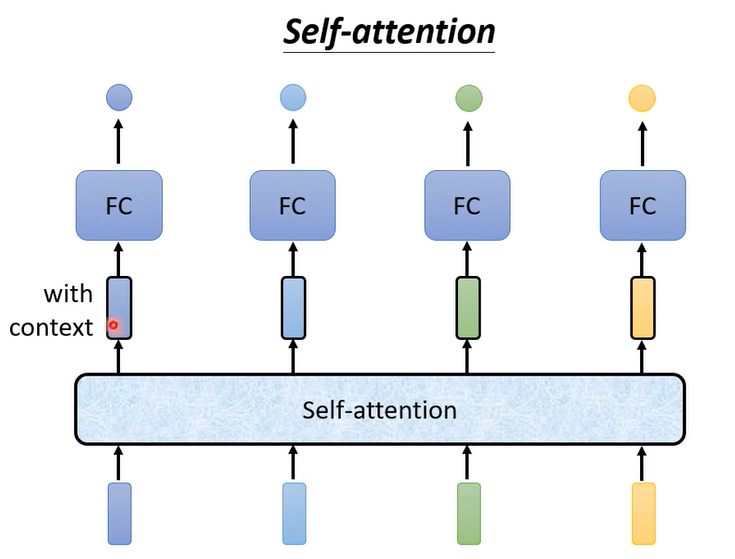
    • image.png
    • 在上图的模型中，self-attention用于处理全部的输入（即处理上下文信息），FC层用于专注于处理某个位置的信息。
    • self-attention层也可以叠加
  • self-attention层内的结构
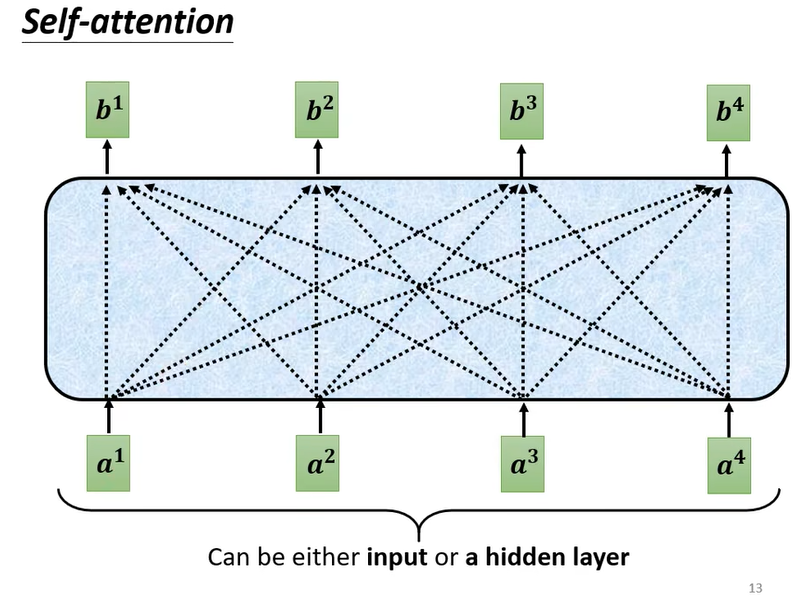
    • image.png
    • 输入元素之间互相计算相关性得到输出
  • self-attention的计算方法：向量点积
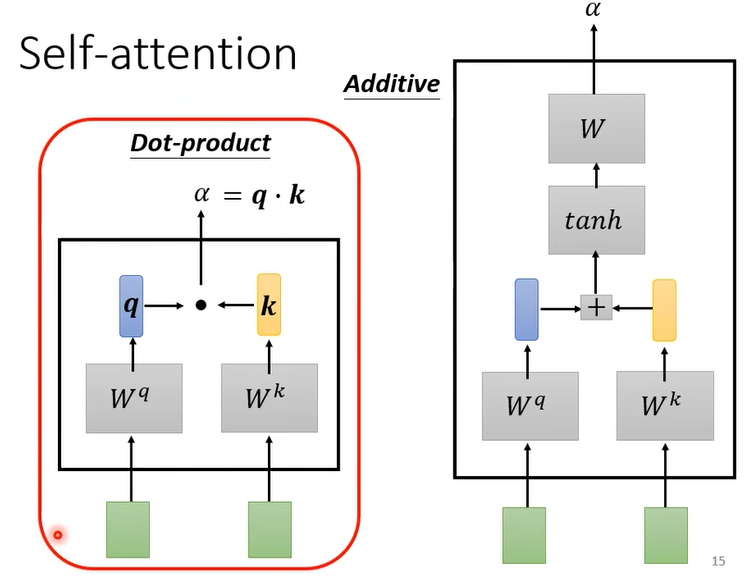
    • image.png
    • 主要以左图为主；右图的加性模型用得少。
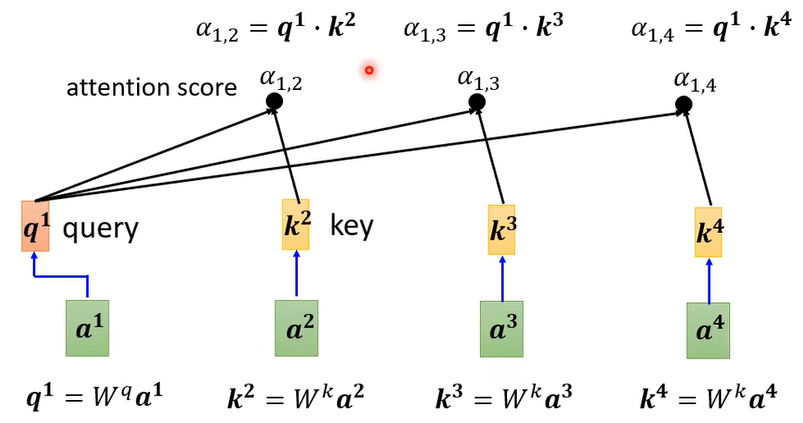
    • 计算方法：首先计算q和k的点积 image.png
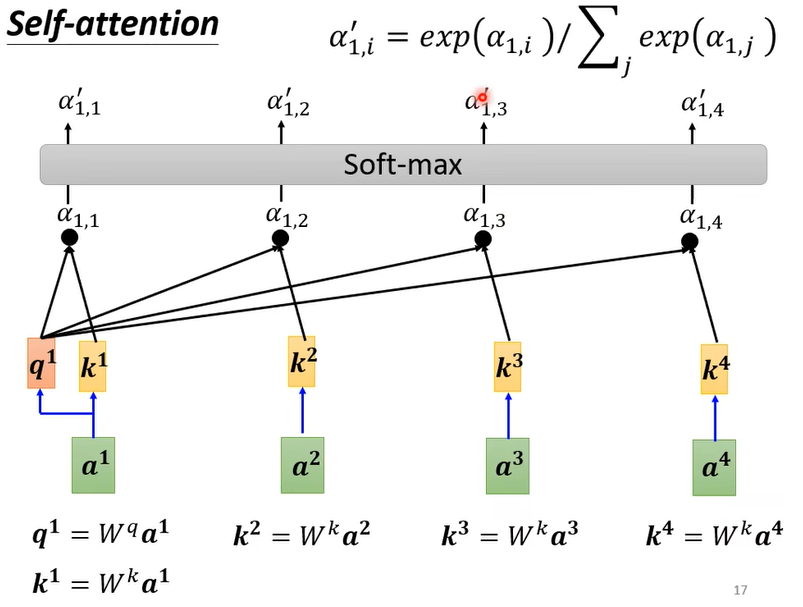
    • 然后计算softmax。这一步得到的就是所谓的注意力分数（attention score） image.png
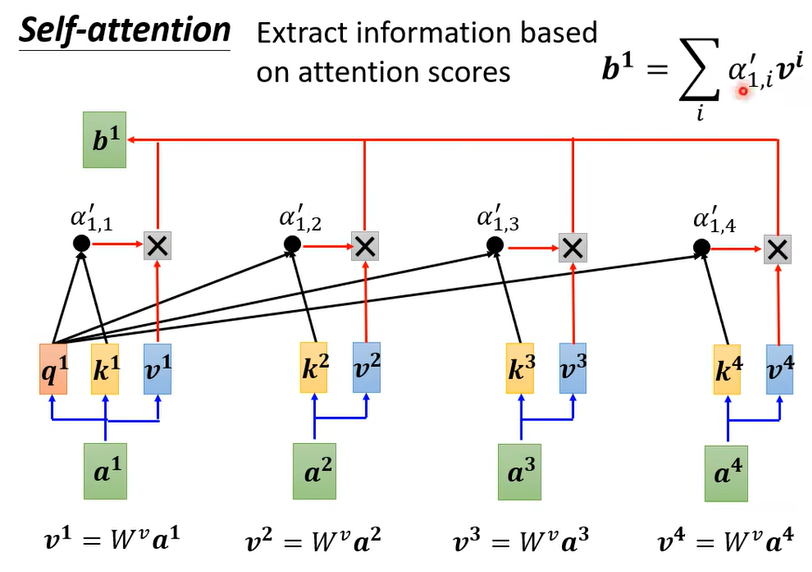
    • 最后和v做叉积 image.png
    • 如上图。我们要计算输入向量 $a^1$ 的输出 $b^1$ ，首先对于输入的向量序列$[a^1,a^2,a^3,a^4]$ 分别计算 $K,\ Q,\ V$ 三个矩阵，然后将输入向量 $a^1$ 的 $q^1$ 与 $[k^1,k^2,k^3,k^4]$ 分别做点乘，点乘结果 $[\alpha’_{1,1},\alpha’_{1,2},\alpha’_{1,3},\alpha’_{1,4}]$ 再与 $[v^1,v^2,v^3,v^4]$ 做叉乘，之后做softmax并相加，即可得到 $b^1$ 。同理， $[b^2,b^3,b^4]$ 也可以通过类似的方法依次计算。
      • 三个矩阵： $K=[k^1,k^2,k^3,k^4],\ Q=[q^1,q^2,q^3,q^4],\ V=[v^1,v^2,v^3,v^4]$

（三）self-attention计算方法的矩阵表示：

我们以一个长度为4的输入序列为例。用矩阵 $I=[a^1,a^2,a^3,a^4]$ 代表这个输入序列，其中 $a^i$ 向量代表序列中第 $i$ 个元素。矩阵 $I$ 的列数为4，代表输入序列中的4个元素；矩阵的行数在这里不重要，所以不做假设。

1. 将输入矩阵 $I$ 映射为 $Q,\ K,\ V$ 三个矩阵

$$
\begin{aligned}
q^i=W^qa^i \\
k^i=W^ka^i \\
v^i=W^va^i \\
\end{aligned}
$$

其中， $W^q,\ W^k,\ W^v$ 都是可学习的参数

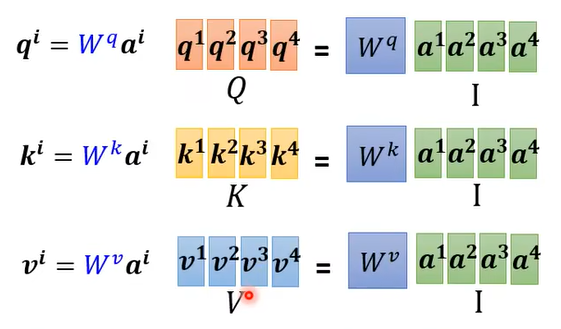
image.png

2. $Q,\ K,\ V$ 三个矩阵的处理

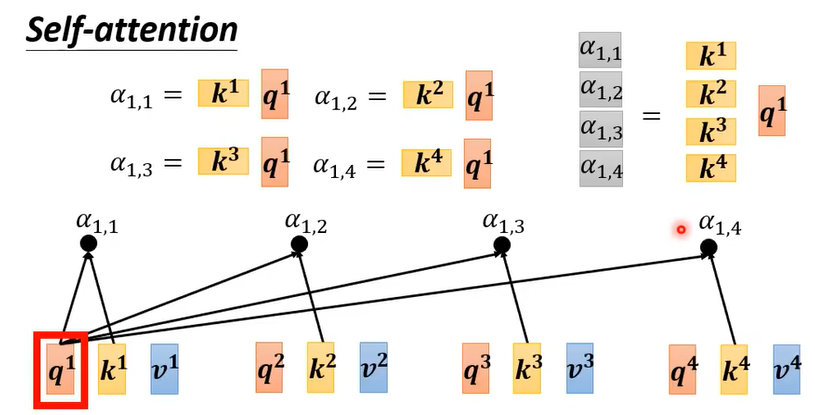
image.png

$q^1$ 的处理如上图，将其分别与 $k^1,k^2,k^3,k^4$ 做点乘，得到 $\alpha_{1,1},\alpha_{1,2},\alpha_{1,3},\alpha_{1,4}$ 。

image.png

对整个输入矩阵$Q$ ， 即 $[q^1,q^2,q^3,q^4]$ 来说，其处理则如上图所示，这个过程可以概括为

$$
A=K^TQ
$$

其中

$$
A=\left[
\begin{aligned}
& \alpha_{1,1},\ \alpha_{2,1},\ \alpha_{3,1},\ \alpha_{4,1} \\
& \alpha_{1,2},\ \alpha_{2,2},\ \alpha_{3,2},\ \alpha_{4,2} \\
& \alpha_{1,3},\ \alpha_{2,3},\ \alpha_{3,3},\ \alpha_{4,3} \\
& \alpha_{1,4},\ \alpha_{2,4},\ \alpha_{3,4},\ \alpha_{4,4} \\
\end{aligned}
\right]
$$

另外，矩阵 $A$ 在进行下一步处理前，还需要经过softmax的处理

$$
A’=\text{softmax}(A)
$$

这一步得到的矩阵 $A’$ 是所谓的注意力分数（attention score），代表了组成输入矩阵的不同向量之间的匹配度。

3. 输出向量的获得

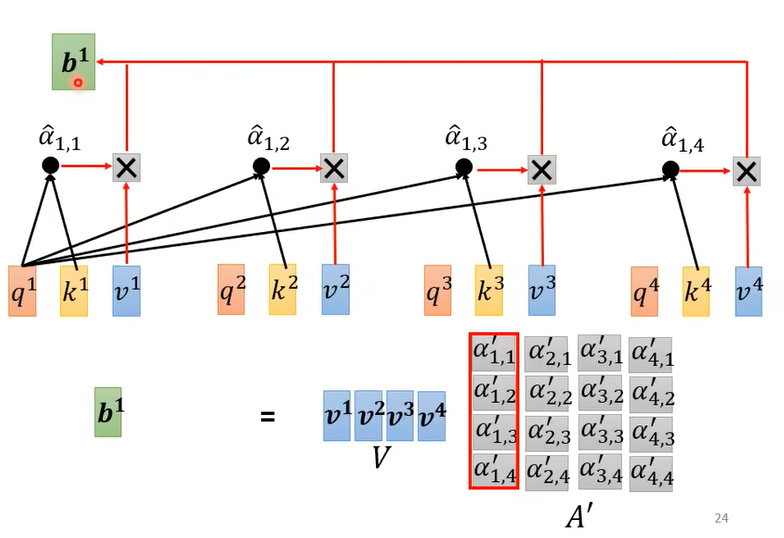
image.png

如上图（纠正一处错误，上图中 $\hat\alpha_{1,1}$ 应该改为 $\alpha’_{1,1}$ ，另外3个符号同理），即self-attention的输出为

$$
O=VA’
$$

其中 $O=[b^1,b^2,b^3,b^4]$ 。

注意，self-attention的输出是一个向量，这个向量的每一个元素代表输入矩阵中的一列向量。（例如， $b^1$ 元素代表输入矩阵中 $a^1$ 这个向量的输出）

总结一下，self-attention的操作如下：

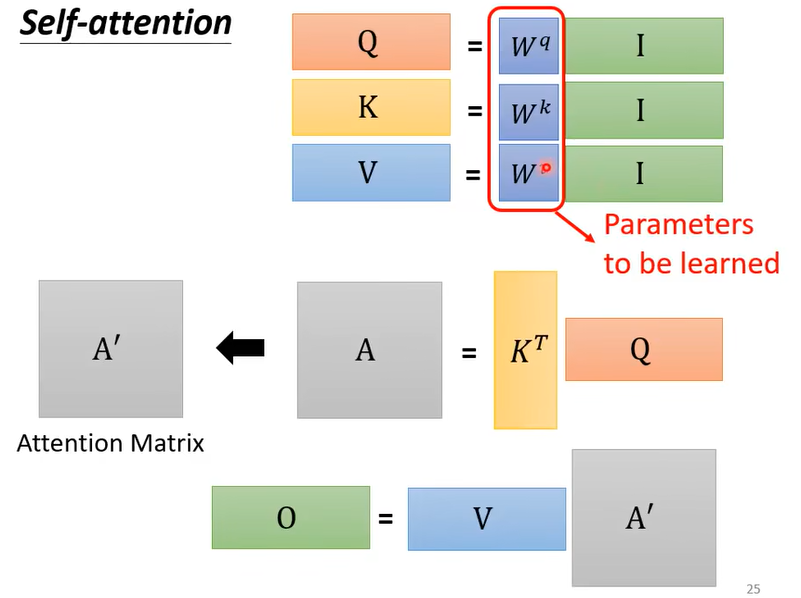
image.png

$$
\begin{aligned}
Q&=W^qI \\
K&=W^kI \\
V&=W^vI \\
O&=V\times \text{softmax}(K^TQ)
\end{aligned}
$$

$I$ 代表输入矩阵，$O$ 代表输出向量。

需要学习的参数只有三个： $W^q,\ W^k,\ W^v$ 。

（四）多头注意力机制（multi-head self-attention）

当我们想要计算输入序列中多种不同的自相关性时，多头注意力机制非常有用。

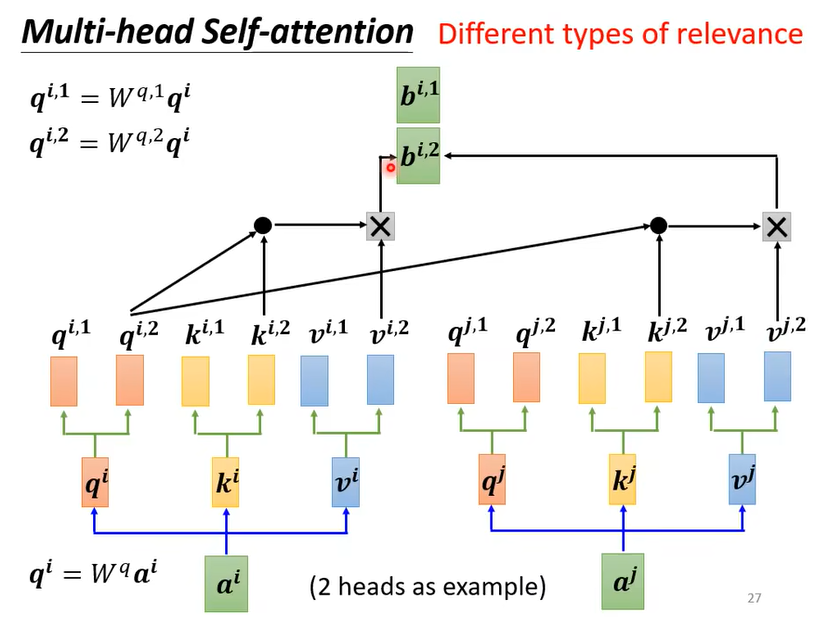
image.png

例如上图，输入序列经过了两个注意力头（attention head）的处理，对于 $a^i$ 这个位置的输入，可以得到两个输出 $[b^{i,1},b^{i,2}]^T$ 。这个输出还可以经过全连接层（FC layer）或其他层进一步处理。

（五）其他变种

1. 位置编码（position encoding）

原生self-attention并不考虑位置信息。然而，在某些任务中，输入元素的位置可能携带了重要信息（例如，在英文词性标注任务中，动词不太可能出现在句首）。

可以使用一些方法将位置信息编码进去，如下图，第 $i$ 个元素的输入等于 $e^i+a^i$ ，其中 $e^i$ 是位置编码。

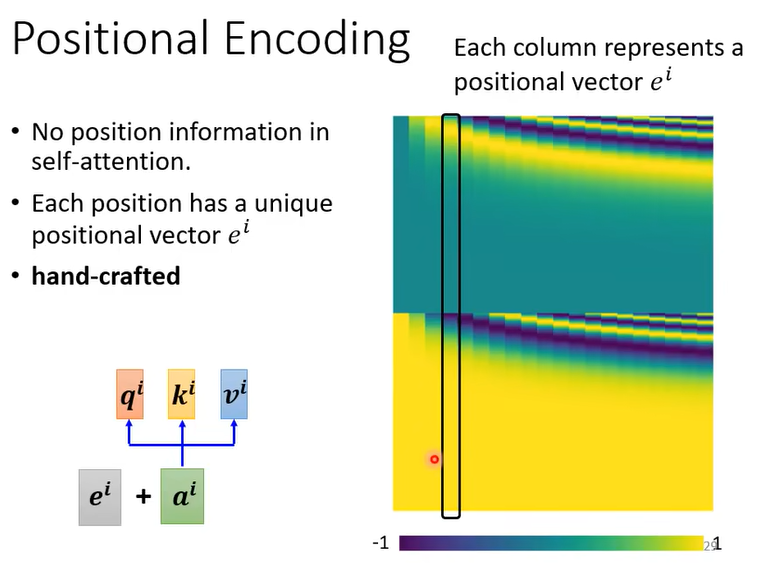
image.png

但是位置编码的方法还有很大的研究空间（例如可以使用sin函数，可以使用另一个模型学习出来，也可以用RNN等），下面展示了研究论文中报导的一些位置编码的方法。

image.png

2. 截断的自注意力（Truncated Self-attention）

在语音识别任务中，输入的音频信号按一定长度的帧进行分割，得到的输入序列长度 $L$ 可能会是一个很大的数字，这意味着做self-attention时需要进行 $L\times L$ 次点乘操作，其计算量过于巨大。Truncated Self-attention则可以解决这个问题。

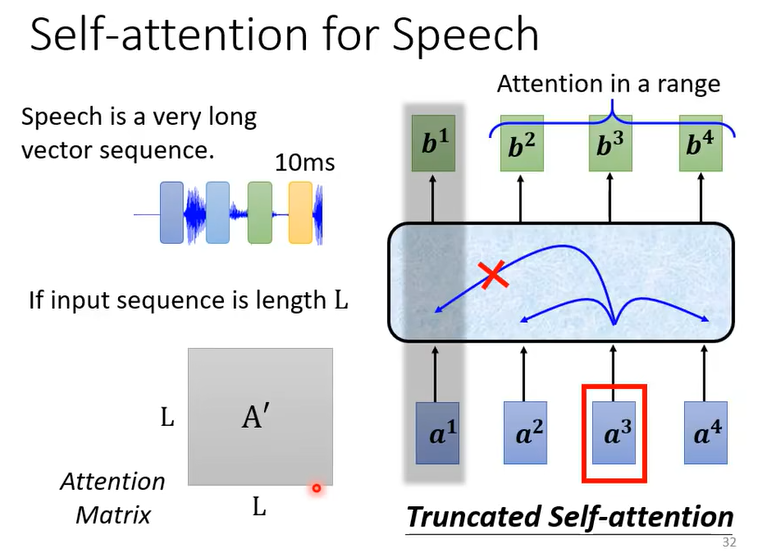
image.png

如上图，在进行Truncated Self-attention时，我们只计算一段范围内的元素的attention。具体看多大范围的元素，可以人为预设。

3. 用于图片的自注意力机制

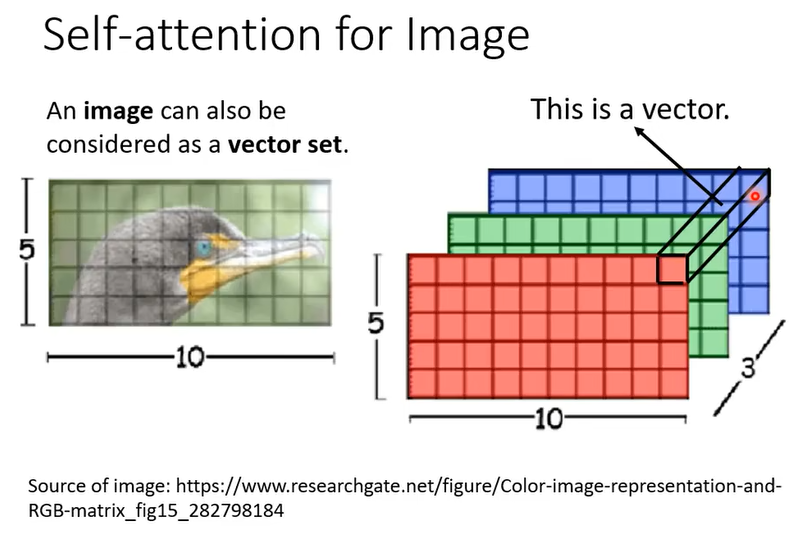
image.png

我们同样可以可以将图片看作vector set（如上图），并对每个像素（即每个vector）进行self-attention处理。

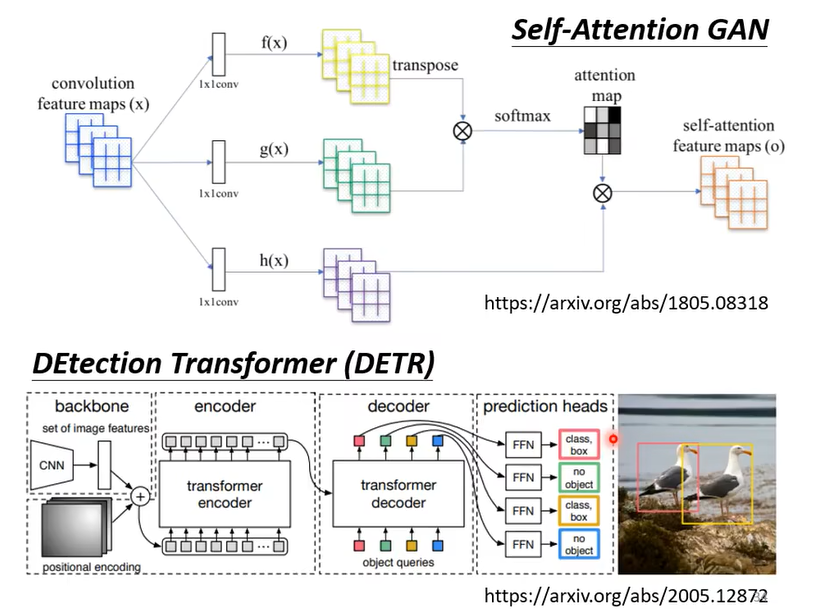
image.png

上图是已发表的一种用于图像的attention。

image.png

我们可以对比一下self-attention和卷积神经网络（CNN）。在处理一个像素时，self-attention考虑的是这个像素与整张图片的关系，而CNN考虑的则是这个像素与卷积核扫过的一小片区域中的像素的关系。可以理解为，CNN是简化的self-attention（或者说，是一种特例），而self-attention是更复杂的CNN。

An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale ：Transformer在图像识别中的应用，并且作者发现训练集越大，Transformer表现越好

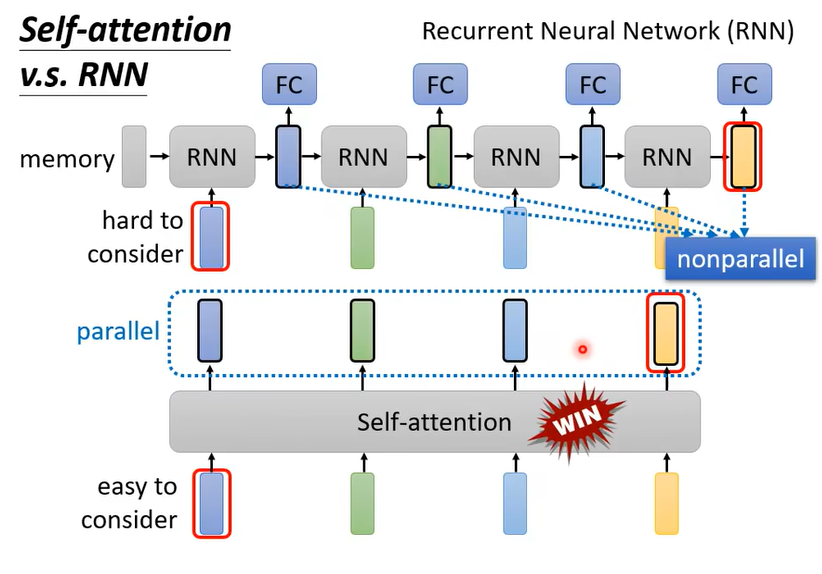
4. self-attention与循环神经网络（RNN）的对比

self-attention与循环神经网络（RNN）都可以用于处理序列数据，但是RNN只能按序列顺序串行处理，依次处理输入数据；而self-attention则可以并行处理。

此外，RNN存在长时程遗忘的问题（在处理序列的最后一个元素时，来自第一个元素的信息有很高的概率会丢失），而self-attention不存在长时程遗忘，在处理任何一个位置的元素时，来自输入序列中的每个元素对于它来说都是一视同仁的。

image.png